关于如何在本地运行Gekko优化的逐步指南
我对编程很陌生,我的第一个Python项目是非线性编程。我正在使用的Gekko优化套件,我有一切正常运行,但需要指导如何准确地在本地运行它。下面是文档所提供的解释和代码,但是我需要一些帮助来帮助我自己如何准确地完成它,以及它到底意味着什么。请表现得像在向小孩子或金毛猎犬解释一样。
run目录m.path包含模型文件gk0_model.apm以及远程(默认)或本地(m=GEKKO(remote=False))运行优化问题所需的其他文件。使用m.open_folder()打开run目录。run目录还包含诊断文件,如如果解决程序找不到解决方案时生成的infeasibilities.txt。可以更改默认的run目录:
from gekko import GEKKO
import numpy as np
import os
# create and change run directory
rd=r'.\RunDir'
if not os.path.isdir(os.path.abspath(rd)):
os.mkdir(os.path.abspath(rd))
m = GEKKO(remote=False) # solve locally
m.path = os.path.abspath(rd) # change run directory回答 1
Stack Overflow用户
发布于 2022-09-20 05:45:04
局部求解
m=GEKKO(remote=False)在本地运行Gekko所需的唯一选项是remote=False。对于remote=False,不需要互联网连接。不需要更改run目录。m.path的默认目录是在临时文件夹中创建的,用于存储编译为字节码的文件。可以使用m.open_folder()访问此文件夹。
基于Intranet服务器的本地解决方案
m=GEKKO(remote=True,server='http://10.0.0.10')有一个APMonitor服务器选项(参见Windows APMonitor服务器或Linux服务器)用于remote=True和server=http://10.0.0.10 (更改为本地Intranet服务器的IP )。这是一个本地计算引擎,运行控制和优化问题的微处理器。这对于没有足够内存或CPU能力来解决优化问题的计算体系结构是有用的,但是当需要在本地解决时。这是一个边缘计算选项,用于在所需的周期时间内完成解决方案(例如,模型预测控制器)。有些组织使用此选项拥有多个连接到一个计算引擎的客户端。可以升级此计算服务器,以便所有客户端自动使用更新的版本。
远程解决
m=GEKKO(remote=True)公共服务器可以作为默认的server选项使用。使用remote=True (默认选项),Gekko将优化问题发送到远程服务器,然后返回解决方案。公共服务器正在运行一个Linux服务器,但是附加的解决器选项由于分发限制而不在本地选项中。
示例Gekko和Scipy优化最小解决方案
GEKKO是一个用于机器学习和优化混合整数和微分方程(见文件)的package .它与线性、二次、非线性和混合整数规划(LP,QP,NLP,MILP,MINLP)的大规模求解器耦合.操作方式包括参数回归、数据协调、实时优化、动态仿真和非线性预测控制.GEKKO是一个面向对象的Python库,以便于APMonitor的本地执行。下面是一个使用remote=False (本地解决方案模式)的简单优化示例。MacOS、Windows和Linux都有本地选项。其他架构需要使用remote=True选项。
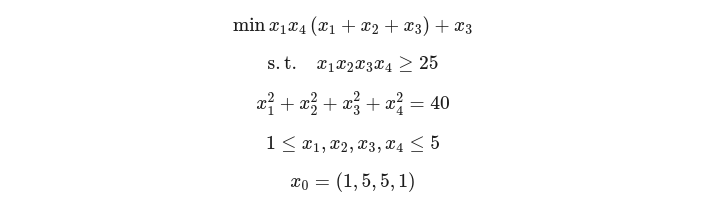
Python
from gekko import GEKKO
m = GEKKO(remote=False)
x = m.Array(m.Var,4,value=1,lb=1,ub=5)
x1,x2,x3,x4 = x
# change initial values
x2.value = 5; x3.value = 5
m.Equation(x1*x2*x3*x4>=25)
m.Equation(x1**2+x2**2+x3**2+x4**2==40)
m.Minimize(x1*x4*(x1+x2+x3)+x3)
m.solve()
print('x: ', x)
print('Objective: ',m.options.OBJFCNVAL)优化最小化
import numpy as np
from scipy.optimize import minimize
def objective(x):
return x[0]*x[3]*(x[0]+x[1]+x[2])+x[2]
def constraint1(x):
return x[0]*x[1]*x[2]*x[3]-25.0
def constraint2(x):
sum_eq = 40.0
for i in range(4):
sum_eq = sum_eq - x[i]**2
return sum_eq
# initial guesses
n = 4
x0 = np.zeros(n)
x0[0] = 1.0
x0[1] = 5.0
x0[2] = 5.0
x0[3] = 1.0
# show initial objective
print('Initial Objective: ' + str(objective(x0)))
# optimize
b = (1.0,5.0)
bnds = (b, b, b, b)
con1 = {'type': 'ineq', 'fun': constraint1}
con2 = {'type': 'eq', 'fun': constraint2}
cons = ([con1,con2])
solution = minimize(objective,x0,method='SLSQP',\
bounds=bnds,constraints=cons)
x = solution.x
# show final objective
print('Final Objective: ' + str(objective(x)))
# print solution
print('Solution')
print('x1 = ' + str(x[0]))
print('x2 = ' + str(x[1]))
print('x3 = ' + str(x[2]))
print('x4 = ' + str(x[3]))附加示例
还有许多附加的Python中的优化包和附加的Gekko教程和基准问题。另一个例子是混合整数线性规划解决方案。

from gekko import GEKKO
m = GEKKO(remote=False)
x,y = m.Array(m.Var,2,integer=True,lb=0)
m.Maximize(y)
m.Equations([-x+y<=1,
3*x+2*y<=12,
2*x+3*y<=12])
m.options.SOLVER = 1
m.solve()
print('Objective: ', -m.options.OBJFCNVAL)
print('x: ', x.value[0])
print('y: ', y.value[0])APOPT求解器是一种混合整数非线性规划(MINLP)求解器(也解决了MILP问题),并作为MacOS、Linux和Windows的本地求解器包括在内。
https://stackoverflow.com/questions/73781278
复制相似问题

