如何利用Gekko优化电动汽车充电成本?
如何利用Gekko优化电动汽车充电成本?
提问于 2022-10-28 10:50:33
from gekko import GEKKO
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO()
m.options.SOLVER = 1
m.options.IMODE = 3
Num_car = 1
TOU = [64.9,64.9,64.9,64.9,64.9,64.9,64.9,64.9,152.6,239.8,239.8,152.6,239.8,239.8,239.8,239.8,152.6,152.6,152.6,152.6,152.6,152.6,152.6,64.9]
n=len(TOU)
p_i = m.Array(m.Var,(n,Num_car))
input = m.Array(m.Var, (n), value = 0.0, lb = 0.0, ub = 7.0, integer = True)
SOC_t = m.Array(m.Var,(n, Num_car))
for tt in range(0,n):
for i in range(0,Num_car):
SOC_t[tt,i].lower = 30
SOC_t[tt,i].upper = 70
SOC_t[0,0] = 30
eq_car_bat = np.zeros((n))
eq_car_bat = list(eq_car_bat)
for tt in range(0,n):
eq_car_bat[tt] = SOC_t[tt] + input[tt] == p_i[tt]
m.Equation(eq_car_bat)
SOC_Max = 90
SOC_Min = 30
sum_soc = sum(SOC_t[tt])
eq_total = np.zeros((n))
eq_total = list(eq_total)
eq_total = sum_soc == SOC_Max
m.Equation(eq_total)
for i in range(n):
m.Minimize(TOU[i]*p_i[i])
m.options.IMODE = 3
m.options.SOLVER = 1
m.solve(disp=True)我想找到最小的收费成本时,电动汽车充电。我的代码如下所示,但我收到了以下错误:"x必须是一个包含GEKKO参数、变量或表达式的python列表“,我不知道如何解决。
回答 1
Stack Overflow用户
发布于 2022-10-28 13:47:41
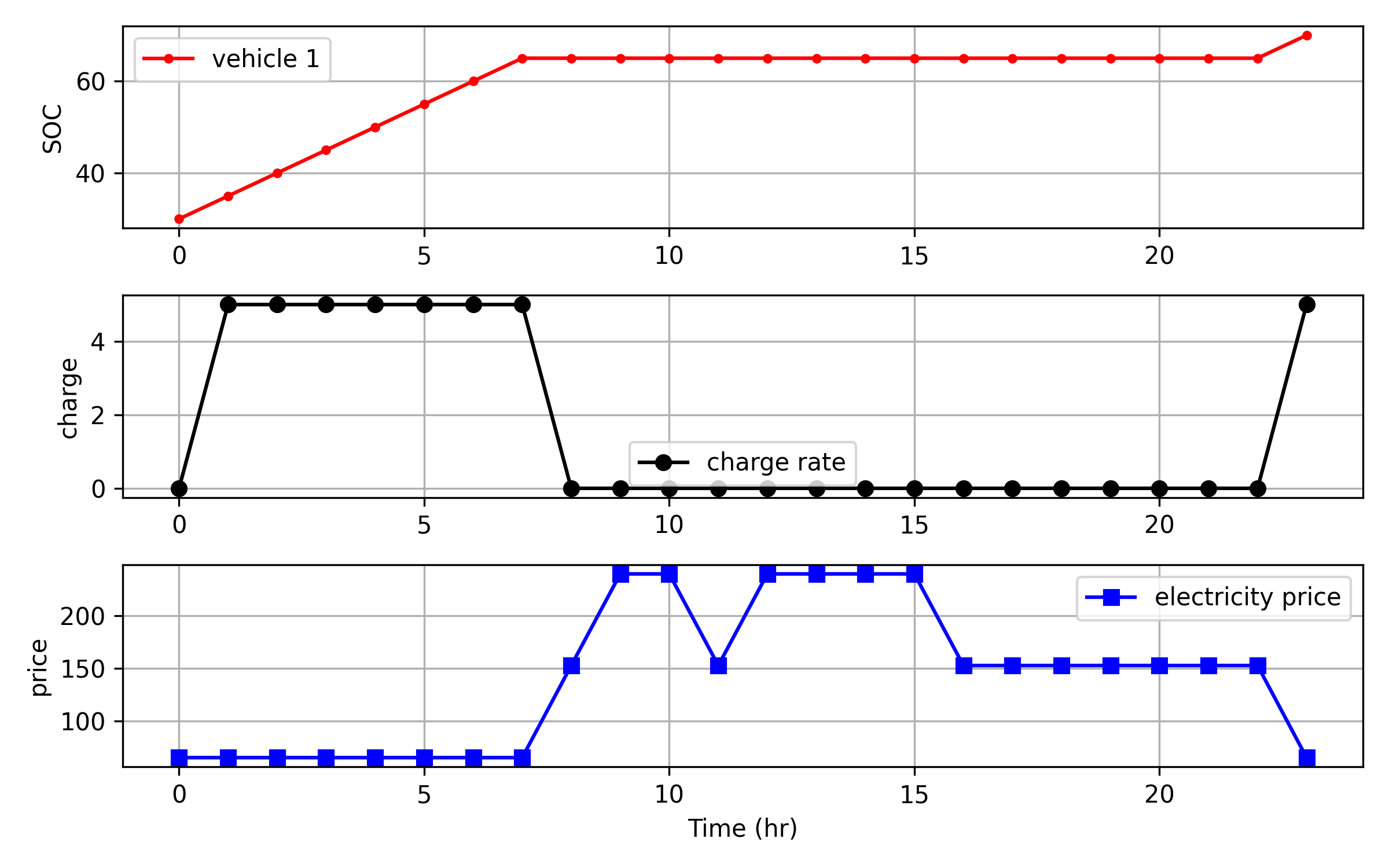
其意图似乎是在特定使用时间(TOU)的情况下,决定何时在24小时内给电池充电。下面是脚本的修改版本,从30到70向SOC收费(整数值0-7)。它有能力增加更多车辆,但目前只有一辆。
from gekko import GEKKO
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO()
m.options.SOLVER = 1
m.options.IMODE = 3
Num_car = 1
TOU = [64.9,64.9,64.9,64.9,64.9,64.9,64.9,64.9,152.6,239.8,
239.8,152.6,239.8,239.8,239.8,239.8,152.6,152.6,
152.6,152.6,152.6,152.6,152.6,64.9]
n=len(TOU)
inp = m.Array(m.Var, (n), value = 0.0,
lb = 0.0, ub = 7.0, integer = True)
SOC_Min = 30; SOC_Max = 90
# set bounds 30-90
SOC_t = m.Array(m.Var,(n, Num_car),lb=SOC_Min,ub=SOC_Max)
# set new bounds 30-70
for tt in range(0,n):
for j in range(Num_car):
SOC_t[tt,j].lower = 30
SOC_t[tt,j].upper = 70
for j in range(Num_car):
# initial SOC
m.Equation(SOC_t[0,j]==30) # initial charge at start
m.Equation(SOC_t[n-1,j]==70) # desired charge at end
for tt in range(1,n):
m.Equation(SOC_t[tt,j] == SOC_t[tt-1,j] + inp[tt])
for tt in range(n):
m.Minimize(TOU[tt]*inp[tt])
m.options.IMODE = 3
m.options.SOLVER = 1
m.solve(disp=True)
plt.figure(figsize=(8,5))
plt.subplot(3,1,1)
for j in range(Num_car):
p = np.empty(n)
for tt in range(n):
p[tt] = SOC_t[tt,j].value[0]
plt.plot(p,'r.-',label='vehicle '+str(j+1))
plt.legend(); plt.ylabel('SOC'); plt.grid()
plt.subplot(3,1,2)
p = np.empty(n)
for tt in range(n):
p[tt] = inp[tt].value[0]
plt.plot(p,'ko-',label='charge rate')
plt.legend(); plt.ylabel('charge'); plt.grid()
plt.subplot(3,1,3)
plt.plot(TOU,'bs-',label='electricity price')
plt.ylabel('price'); plt.grid()
plt.legend(); plt.xlabel('Time (hr)')
plt.tight_layout()
plt.savefig('soc_results.png',dpi=300)
plt.show()这个问题与能源基准中的其他一些问题有关。当使用IMODE=6而不是显式索引时间时,Gekko能够管理问题的时间方面。使用IMODE=3 (默认)可以更好地控制问题结构。如果有微分方程的话,IMODE=6更好。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/74234285
复制相关文章
相似问题

