用leasqr算法拟合复杂数据时的误差
我有数据作为复数的实部和虚部,我想根据复变函数对它们进行拟合。更详细地说,它们是来自电化学阻抗谱(EIS)实验的数据,其功能来自等效电路。我在Windows 10电脑上使用Octave 7.2.0。我需要使用Optim中的leasqr算法。leasqr采用了典型的EIS数据拟合的Levenberg-Marquardt非线性回归。对于数据,xdata为线性频率,y数据为ReZ + j*ImZ。如果我尝试用复拟合函数对复杂数据进行拟合,则会得到以下错误:
error: weighted residuals are not real
error: called from
__lm_svd__ at line 147 column 20
leasqr at line 662 column 25
Code_for_StackOverflow at line 47 column 73我试着用拟合函数的实部拟合数据的实部,用函数的虚部拟合数据的虚部。配合成功,但我有两套合适的参数,而我只需要一套。这是我写的代码。
clear -a;
clf;
clc;
pkg load optim;
pkg load symbolic;
Linear_freq = [1051.432, 394.2871, 112.6535, 39.42871, 11.59668, 3.458659, 1.065641, 0.3258571, 0.1000221];
ReZ = [84.10412, 102.0962, 178.8031, 283.0663, 366.7088, 431.3653, 514.4105, 650.5853, 895.9588];
MinusImZ = [27.84804, 59.56786, 116.5972, 123.2293, 102.6806, 117.4836, 178.1147, 306.256, 551.2337];
Z = [88.5946744, 118.2030626, 213.4606653, 308.7264008, 380.8131426, 447.0776424, 544.3739605, 719.0646495, 1051.950932];
MinusPhase = [18.32042302, 30.26135402, 33.1083029, 23.52528583, 15.64255593, 15.23515301, 19.09841797, 25.2082044, 31.60167787];
ImZ = -MinusImZ;
Angular_freq = 2*pi*Linear_freq;
xdata = Angular_freq;
ydata = ReZ + j*ImZ;
Fitting_Function = @(xdata, p) (p(1) + ((p(2) + (1./(p(3)*(j*xdata).^0.5))).^-1 + (1./(p(4)*(j*xdata).^p(5))).^-1).^-1);
p = [80, 300, 6.63E-3, 5E-5, 0.8]; # True parameters values, taken with a dedicated software: 76, 283, 1.63E-3, 1.5E-5, 0.876
options.fract_prec = [0.0005, 0.0005, 0.0005, 0.0005, 0.0005].';
niter=400;
tol=1E-12;
dFdp="dfdp";
dp=1E-9*ones(size(p));
wt = abs(sqrt(ydata).^-1);
#[Fitted_Parameters_ReZ pfit_real cvg_real iter_real corp_real covp_real covr_real stdresid_real z_real r2_real] = leasqr(xdata, ReZ, p, Fitting_Function_ReZ, tol, niter, wt, dp, dFdp, options);
#[Fitted_Parameters_ImZ pfit_imag cvg_imag iter_imag corp_imag covp_imag covr_imag stdresid_imag z_imag r2_imag] = leasqr(xdata, ImZ, p, Fitting_Function_ImZ, tol, niter, wt, dp, dFdp, options);
[Fitted_Parameters pfit cvg iter corp covp covr stdresid z r2] = leasqr(xdata, ydata, p, Fitting_Function, tol, niter, wt, dp, dFdp, options);
#########################################################################
# Calculate the fitted functions, with the fitted paramteres array
#########################################################################
Fitted_Function_Real = real(pfit_real(1) + ((pfit_real(2) + (1./(pfit_real(3)*(j*xdata).^0.5))).^-1 + (1./(pfit_real(4)*(j*xdata).^pfit_real(5))).^-1).^-1);
Fitted_Function_Imag = imag(pfit_imag(1) + ((pfit_imag(2) + (1./(pfit_imag(3)*(j*xdata).^0.5))).^-1 + (1./(pfit_imag(4)*(j*xdata).^pfit_imag(5))).^-1).^-1);
Fitted_Function = Fitted_Function_Real + j.*Fitted_Function_Imag;
Fitted_Function_Mod = abs(Fitted_Function);
Fitted_Function_Phase = (-(angle(Fitted_Function))*(180./pi));
################################################################################
# Calculate the residuals, from https://iopscience.iop.org/article/10.1149/1.2044210
# An optimum fit is obtained when the residuals are spread randomly around the log Omega axis.
# When the residuals show a systematic deviation from the horizontal axis, e.g., by forming
# a "trace" around, above, or below the log co axis, the complex nonlinear least squares (CNLS) fit is not adequate.
################################################################################
Residuals_Real = (ReZ-Fitted_Function_Real)./Fitted_Function_Mod;
Residuals_Imag = (ImZ-Fitted_Function_Imag)./Fitted_Function_Mod;
################################################################################
# Calculate the chi-squared - reduced value, with the fitted paramteres array NOVA manual page 452
################################################################################
chi_squared_ReZ = sum(((ReZ-Fitted_Function_Real).^2)./Z.^2)
chi_squared_ImZ = sum(((ImZ-Fitted_Function_Imag).^2)./Z.^2)
Pseudo_chi_squared = sum((((ReZ-Fitted_Function_Real).^2)+((ImZ-Fitted_Function_Imag).^2))./Z.^2)
disp('The values of the parameters after the fit of the real function are '), disp(pfit_real);
disp('The values of the parameters after the fit of the imaginary function are '), disp(pfit_imag);
disp("R^2, the coefficient of multiple determination, intercept form (not suitable for non-real residuals) is "), disp(r2_real), disp(r2_imag);
###################################################
## PLOT Data and the Function
###################################################
#Set plot parameters
set(0, "defaultlinelinewidth", 1);
set(0, "defaulttextfontname", "Verdana");
set(0, "defaulttextfontsize", 20);
set(0, "DefaultAxesFontName", "Verdana");
set(0, 'DefaultAxesFontSize', 12);
figure(1);
## Nyquist plot (Argand diagram)
subplot(1,2,1, "align");
plot((ReZ), (MinusImZ), "o", "markersize", 2, (Fitted_Function_Real), -(Fitted_Function_Imag), "-k");
axis ("square");
grid on;
daspect([1 1 2]);
title ('Nyquist Plot - Argand Diagram');
xlabel ('Z'' / \Omega' , 'interpreter', 'tex');
ylabel ('-Z'''' / \Omega', 'interpreter', 'tex');
## Bode Modulus
subplot (2, 2, 2);
loglog((Linear_freq), (Z), "o", "markersize", 2, (Linear_freq), (Fitted_Function_Mod), "-k");
grid on;
title ('Bode Plot - Modulus');
xlabel ('\nu (Hz)' , 'interpreter', 'tex');
ylabel ('|Z| / \Omega', 'interpreter', 'tex');
## Bode Phase
subplot (2, 2, 4);
semilogx((Linear_freq), (MinusPhase), "o", "markersize", 2, (Linear_freq), (Fitted_Function_Phase), "-k");
set(gca,'YTick',0:10:90);
grid on;
title ('Bode Plot - Phase');
xlabel ('\nu (Hz)' , 'interpreter', 'tex');
ylabel ('-\theta (°)', 'interpreter', 'tex');
figure(2)
## Bode Z'
subplot (2, 1, 1);
semilogx((Linear_freq), (ReZ), "o", "markersize", 2, (Linear_freq), (Fitted_Function_Real), "-k");
grid on;
title ('Bode Plot Z''');
xlabel ('\nu (Hz)' , 'interpreter', 'tex');
ylabel ('Z'' / \Omega', 'interpreter', 'tex');
## Bode -Z''
subplot (2, 1, 2);
#subplot (2, 2, 4);
semilogx((Linear_freq), (MinusImZ), "o", "markersize", 2, (Linear_freq), -(Fitted_Function_Imag), "-k");
grid on;
title ('Bode Plot -Z''''');
xlabel ('\nu (Hz)' , 'interpreter', 'tex');
ylabel ('-Z'''' / \Omega', 'interpreter', 'tex');
figure(3)
## Residuals Real
subplot (2, 1, 1);
semilogx((Angular_freq), (Residuals_Real), "-o", "markersize", 2);
grid on;
title ('Residuals Real');
xlabel ('\omega (Hz)' , 'interpreter', 'tex');
ylabel ('\Delta_{re} / \Omega', 'interpreter', 'tex');
## Residuals Imaginary
subplot (2, 1, 2);
#subplot (2, 2, 4);
semilogx((Angular_freq), (Residuals_Imag), "-o", "markersize", 2);
grid on;
title ('Residuals Imaginary');
xlabel ('\omega (Hz)' , 'interpreter', 'tex');
ylabel ('\Delta_{im} / \Omega', 'interpreter', 'tex');八度应该能够处理复数。我做错什么了?我想用拟合函数的实部来拟合数据的实部,然后用Kramers-Kronig关系得到拟合函数的虚部,但如果可能的话,我想避免这种方法。
如能提供任何帮助,我们将不胜感激。
回答 1
Stack Overflow用户
发布于 2022-11-13 12:06:18
从您绘制的数据中,复杂的阻抗图显示了一个相当常见的形状,可以用许多等效电路来建模:

参考资料:https://fr.scribd.com/doc/71923015/The-Phasance-Concept
您可能根据一些物理考虑选择了n°2模型。这不是这里要讨论的问题。
此外,根据物理考虑和/或通过图形检查,您正确地假定一个阶段属于Warbourg类(Phi=-pi/4;nu=-1/2)。
问题是拟合一个有五个可调参数的方程。这是复杂方程非线性回归的一个难题。通常的方法是从五个参数的“猜测值”开始的迭代过程。
“猜测值”必须离未知的正确值不远。通过对阻抗图的图形检验,可以得到一些近似的结果。这往往是迭代过程收敛失败的原因之一。
一种更可靠的方法是采用线性回归、wrt和非线性回归相结合的方法,wrt的参数很少。
在此情况下,可以将非线性回归简化为一个参数,而其他参数则可以通过简单的线性回归来处理。这是一个很大的简化。

1980-1990年开发了一个线性和非线性混合回归软件(涉及多个相量的情况)。不幸的是,我现在无法访问它。
然而,在目前的情况下,只有一个相量,我们不需要一个大锤来打破一个螺母。牛顿-拉夫森方法是充分的.图形检查得出(nu)大致在-0.7至-0.8之间,选择的初始值为nu=-0.75,下一轮为:
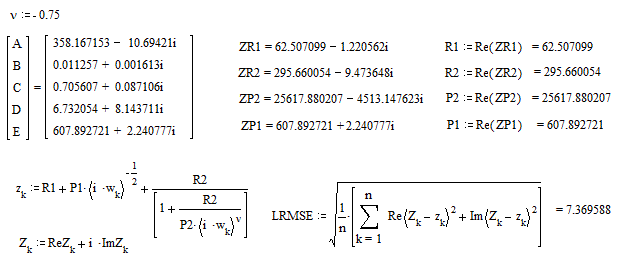
由于所有的演算都是以复数的形式进行的,因此得到的数值是复杂的,而不是像预期的那样是实的。他们被称为ZR1,ZR2,ZP1,ZP2,以区别于真实的R1,R2,P1,P2。这是因为(nu)的值不是最优的。
(nu)越多地收敛到最终值,虚部就越消失。经过几次牛顿-拉夫森过程后,想象的部分变得相当微不足道。最终结果如下所示。

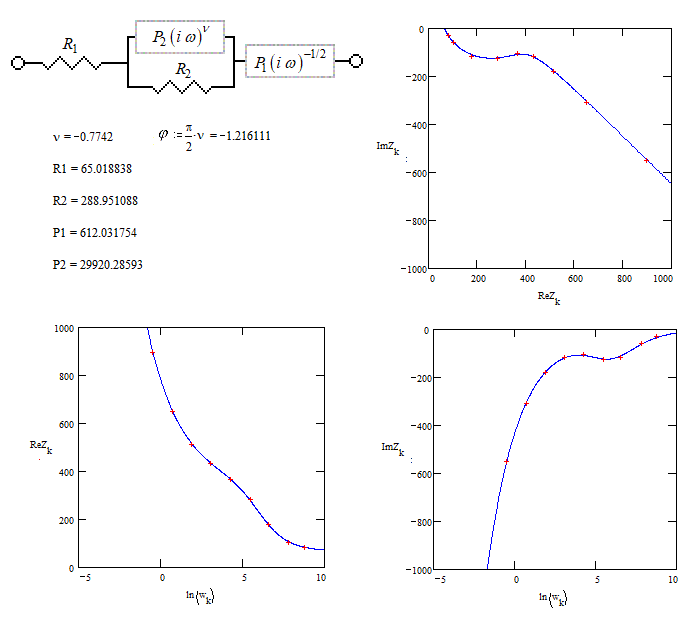
出版物:
“交流会的贡献-确定各项措施”。2-ième Forum sur les Im电子嵌合体,1987年8月28日至29日。
"Calcul de réseauélectriqueséquivalentsàpartir de mesures d‘’impéde“。3-1988年11月24日-Ième Forum sur les Iméles。
"Synthèse de电路électiqueséquivalentsàpartir de mesures d‘’impéde情结“。5-1991年11月28日-Ième Forum sur les Iméles。
https://stackoverflow.com/questions/74347221
复制相似问题

