Python中的指数回归
我有一组x和y数据,我想使用指数回归来找到最适合这些点集的直线。即:
y = P1 + P2 exp(-P0 x)我要计算P0、P1和P2的值。
我使用了一个软件"Igor Pro“来计算我的值,但是我想要一个Python实现。我使用了curve_fit函数,但得到的值与Igor软件计算的值相差甚远。以下是我拥有的一组数据:
Set1:
x = [ 1.06, 1.06, 1.06, 1.06, 1.06, 1.06, 0.91, 0.91, 0.91 ]
y = [ 476, 475, 476.5, 475.25, 480, 469.5, 549.25, 548.5, 553.5 ]Igor计算的数值:
P1=376.91, P2=5393.9, P0=3.7776由curve_fit计算的数值
P1=702.45, P2=-13.33. P0=-2.6744Set2:
x = [ 1.36, 1.44, 1.41, 1.745, 2.25, 1.42, 1.45, 1.5, 1.58]
y = [ 648, 618, 636, 485, 384, 639, 630, 583, 529]Igor计算的数值:
P1=321, P2=4848, P0=-1.94由curve_fit计算的值:
No optimal values found我使用curve_fit的方式如下:
from scipy.optimize import curve_fit
popt, pcov = curve_fit(lambda t, a, b, c: a * np.exp(-b * t) + c, x, y)其中:
P1=c, P2=a and P0=b回答 3
Stack Overflow用户
发布于 2022-12-02 04:31:28
那么,在比较拟合结果时,在拟合参数中包含不确定性总是很重要的。也就是说,当您说来自Igor (P1=376.91,P2=5393.9,P0=3.7776)和curve_fit (P1=702.45,P2=-13.33 )的值。P0=-2.6744)是不同的,是什么导致了这些值实际上是不同的?
当然,在日常的谈话中,376.91和702.45是非常不同的,主要是因为简单地表示小数点2位的值意味着在这个比例上的准确性(纽约和东京之间的距离是10,850公里,但实际上不是10,847,024,31厘米-这可能是这两个城市公交车站之间的距离)。但是,当比较适合的结果时,日常知识不能被假定,而且你必须包括不确定性。我不知道伊戈尔会不会给你这些。curve_fit是可以的,但是它需要一些工作来提取它们--真遗憾。
请允许我推荐尝试lmfit (免责声明:我是作者)。这样,您就可以像这样设置并执行fit:
import numpy as np
from lmfit import Model
x = [ 1.06, 1.06, 1.06, 1.06, 1.06, 1.06, 0.91, 0.91, 0.91 ]
y = [ 476, 475, 476.5, 475.25, 480, 469.5, 549.25, 548.5, 553.5 ]
# x = [ 1.36, 1.44, 1.41, 1.745, 2.25, 1.42, 1.45, 1.5, 1.58]
# y = [ 648, 618, 636, 485, 384, 639, 630, 583, 529]
# Define the function that we want to fit to the data
def func(x, offset, scale, decay):
return offset + scale * np.exp(-decay* x)
model = Model(func)
params = model.make_params(offset=375, scale=5000, decay=4)
result = model.fit(y, params, x=x)
print(result.fit_report())这将打印出
[[Model]]
Model(func)
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 49
# data points = 9
# variables = 3
chi-square = 72.2604167
reduced chi-square = 12.0434028
Akaike info crit = 24.7474672
Bayesian info crit = 25.3391410
R-squared = 0.99362489
[[Variables]]
offset: 413.168769 +/- 17348030.9 (4198775.95%) (init = 375)
scale: 16689.6793 +/- 1.3337e+10 (79909638.11%) (init = 5000)
decay: 5.27555726 +/- 1016721.11 (19272297.84%) (init = 4)
[[Correlations]] (unreported correlations are < 0.100)
C(scale, decay) = 1.000
C(offset, decay) = 1.000
C(offset, scale) = 1.000这表明参数值中的不确定性是巨大的,所有参数之间的相关性都是1。这是因为只有2个x值,这使得无法准确地确定3个自变量。
而且,请注意,当不确定性为1700万时,P1 (抵消)值为413和762实际上是一致的。问题不是伊戈尔和curve_fit在最佳值上意见不一致,而是两者都不能精确地确定这个值。
对于其他数据集,情况稍微好一点,结果是:
[[Model]]
Model(func)
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 82
# data points = 9
# variables = 3
chi-square = 1118.19957
reduced chi-square = 186.366596
Akaike info crit = 49.4002551
Bayesian info crit = 49.9919289
R-squared = 0.98272310
[[Variables]]
offset: 320.876843 +/- 42.0154403 (13.09%) (init = 375)
scale: 4797.14487 +/- 2667.40083 (55.60%) (init = 5000)
decay: 1.93560164 +/- 0.47764470 (24.68%) (init = 4)
[[Correlations]] (unreported correlations are < 0.100)
C(scale, decay) = 0.995
C(offset, decay) = 0.940
C(offset, scale) = 0.904相关系数仍然很高,但参数确定得比较好。另外,请注意,这里的最佳拟合值与您从Igor获得的值更接近,而且可能“在不确定性范围内”。
这就是为什么一个总是需要包含由fit报告的最佳拟合值的不确定性。
Stack Overflow用户
发布于 2022-12-02 11:06:30
第1组:
X= 1.06,1.06,1.06,1.06,1.06,1.06,0.91,0.91,0.91
Y= 476,475,476.5,475.25,480,469.5,549.25,548.5,553.5
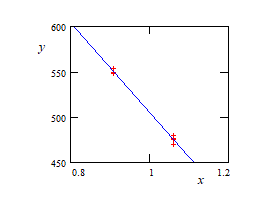
有人指出,它们只是x: 1.06和0.91的两个不同的值。
另一方面,它们是三个需要优化的参数: P0、P1和P2。这太过分了。
换句话说,指数曲线的无穷大可以用来拟合这两个点簇。曲线之间的差异可能是由于非线性回归计算方法的细微差异,特别是由于选择迭代过程初始值的方法。
在这种情况下,简单的线性回归是没有歧义的。
相比之下:
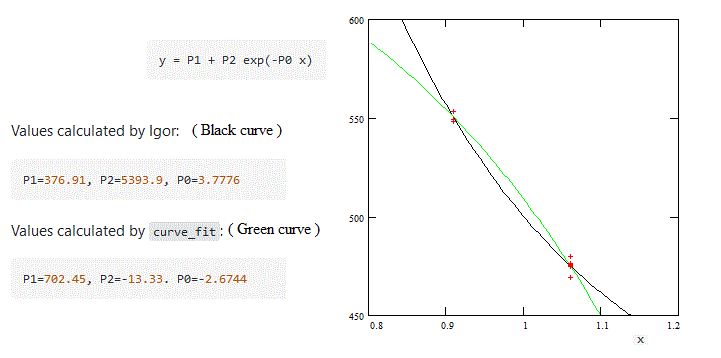
因此,Igor和Curve_fit都给出了很好的拟合:点非常接近两条曲线。一个人知道无穷大,许多其他的指数函数也适用。
第2组:
X= 1.36、1.44、1.41、1.745、2.25、1.42、1.45、1.5、1.58
Y= 648,618,636,485,384,639,630,583,529
您遇到的困难可能是由于选择了“猜测”的参数初始值,这些参数是开始非线性回归迭代过程所必需的。
为了检验这个假设,我们可以使用另一种方法,它不需要初始的猜测值。MathCad代码和数值演算如下所示。
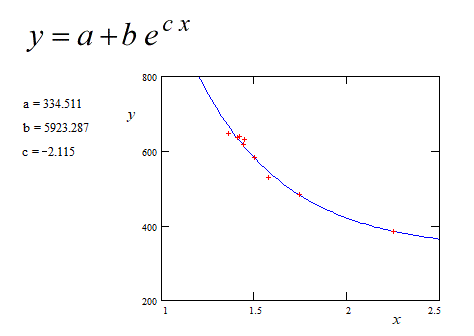
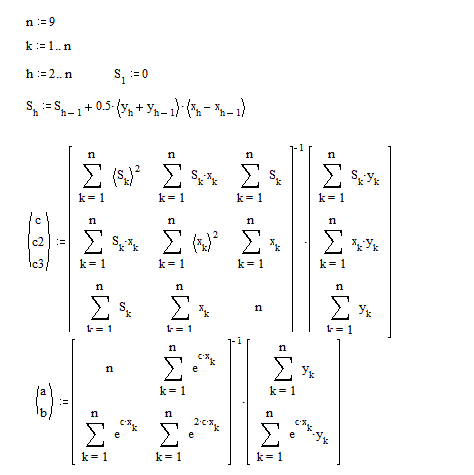
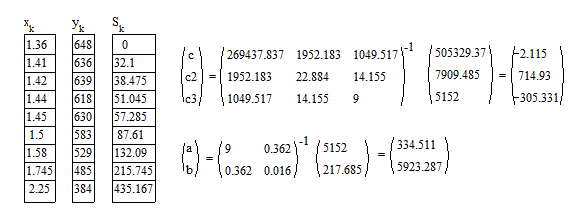
如果您在软件中获得的参数值与上述值(a、b、c)略有不同,请不要感到惊讶。在您的软件中隐式设置的拟合标准可能与我的软件中的拟合集标准不同。
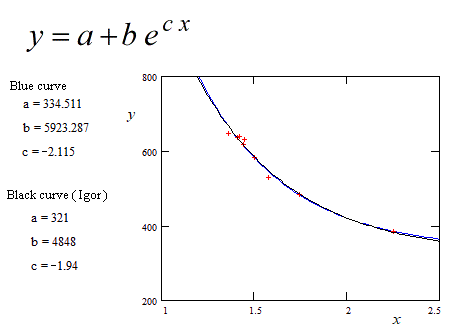
蓝色曲线:回归的方法是最小均方误差,wrt是指数方程解的线性积分方程。参考文献:https://fr.scribd.com/doc/14674814/Regressions-et-equations-integrales
这种非标准方法不是迭代的,不需要参数的初始“猜测”值。
Stack Overflow用户
发布于 2022-12-01 19:58:40
看起来,curve_fit函数不是解决这个问题的合适工具,因为您试图将数据拟合到(y = P1 + P2 * exp(-P0 * x))的函数有三个参数,而curve_fit则期望一个只有一个参数的函数(在本例中是自变量)。您可以使用curve_fit来用t和单个参数表示y来拟合数据的单参数函数,但这不会给出您想要的P1、P2和P0的值。
要使这个特定的函数适合您的数据,您需要使用不同的方法。一种可能的方法是定义一个函数,它以x、P1、P2和P0作为参数,并根据上面的方程返回y的对应值。然后,您可以使用非线性优化算法来找到P1、P2和P0的值,从而最小化数据中y的预测值与y的观测值之间的差异。有几个Python库提供了可用于此目的的非线性优化算法,如scipy.optimize和lmfit。
下面是一个示例,说明如何使用scipy.optimize将数据与函数y= P1 + P2 * exp(-P0 *x)相匹配:
import numpy as np
from scipy.optimize import minimize
# Define the function that we want to fit to the data
def func(x, P1, P2, P0):
return P1 + P2 * np.exp(-P0 * x)
# Define a function that takes the parameters of the function as arguments
# and returns the sum of the squared differences between the predicted
# and observed values of y
def objective(params):
P1, P2, P0 = params
y_pred = func(x, P1, P2, P0)
return np.sum((y - y_pred) ** 2)
# Define the initial values for the parameters
params_init = [376.91, 5393.9, 3.7776]
# Use the minimize function to find the values of the parameters that
# minimize the objective function
result = minimize(objective, params_init)
# Print the optimized values of the parameters
print(result.x)这段代码应该为P1、P2和P0提供与Igor软件计算的值相同的值。然后,您可以使用参数的优化值来使用上面定义的func函数来预测任意给定值x的y值。
我希望这能帮到你!如果你还有其他问题,请告诉我。
https://stackoverflow.com/questions/74647310
复制相似问题

