当点被拖动时对齐矩形的算法?
当点被拖动时对齐矩形的算法?
提问于 2022-12-02 14:14:20
我正在尝试实现一种算法,当点被拖动时,该算法将对齐椭圆上的矩形。
我掌握的数据如下:
- 我知道哪个角落被拖着
- 它的起始位置
- 它的结尾位置
我以前的算法是对齐相邻的角,但只有当椭圆或矩形不成角时才能对齐。
我正在尝试实现一些像Figma所做的事情:
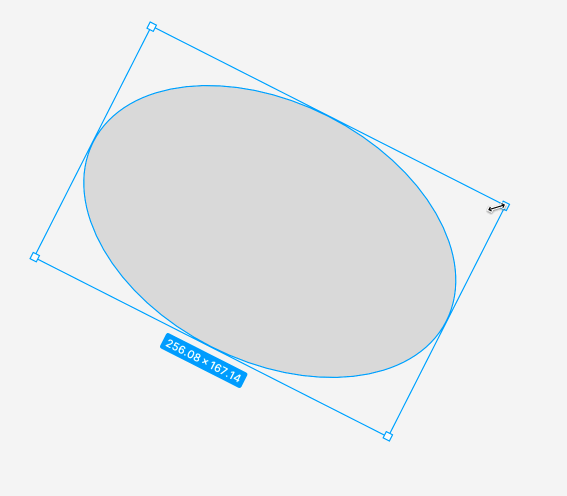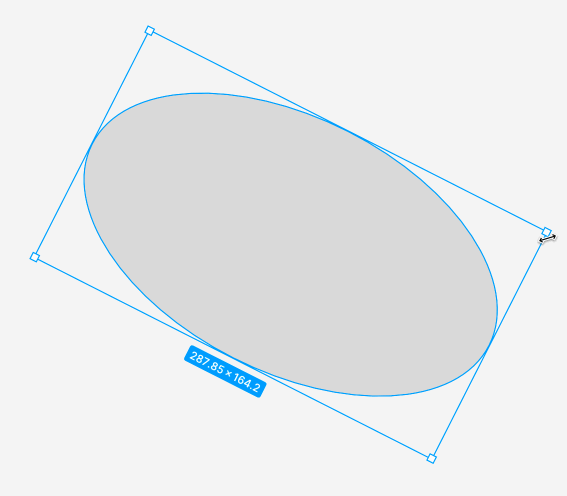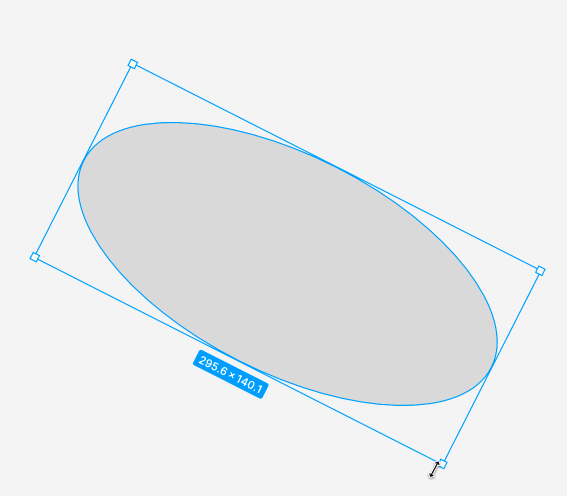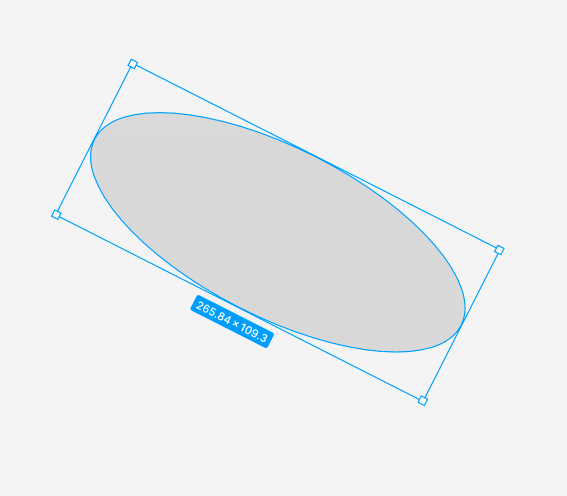
我目前的想法是把那些在拖动时被改变的边和其他没有改变的边匹配到改变的边的大小。但我不确定这是否正确。
回答 1
Stack Overflow用户
回答已采纳
发布于 2022-12-02 17:09:55
用中心点(CX, CY)和两个单位方向向量(WX, WY)和(HX, HY)描述矩形,W是半宽的,H是半高的。
据我所知,矩形斜率是保留的,所以方向向量保持不变。
当角号k被移动时,它的新位置是(NX, NY)。相反的顶点有数字(k+2)%4,它的位置是(PX, PY) (不变)
新中心
CX' = (PX + NX) / 2
CY' = (PY + NY) / 2新半宽半高
W' = 0.5 * Abs(WX * (NX - PX) + WY * (NY - PY))
H' = 0.5 * Abs(HX * (NX - PX) + HY * (NY - PY))页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/74657149
复制相关文章
相似问题

