如何正确地替换FFT的真实部分?
如何正确地替换FFT的真实部分?
提问于 2021-11-30 06:58:04
我尝试复制一种数据增强方法,该方法来自于本文:
徐秦伟,张瑞鹏,张亚章,王燕峰,齐田“基于傅里叶的领域综合框架” (CVPR 2021)。
文中提到,它们将图像的真实部分设为常数(本文中的常数为20000),以消除幅值,实现仅依赖相位的图像重建。下面是我的代码:
img = process_img("./data/house.jpg", 128)
img_fft = torch.fft.fft2(img, dim=(-2, -1))
amp = torch.full(img_fft.shape, 200000)
img_fft.real = amp
img_ifft = torch.fft.ifft2(img_fft, dim=(-2, -1))
img_ifft = img_ifft.squeeze(0)
img_ifft = img_ifft.transpose(2, 0)
img_ifft = np.array(img_ifft)
cv2.imshow("", img_ifft.real)其中,process_img函数仅用于将ndarray转换为张量,如下所示:
loader = transforms.Compose([transforms.ToTensor()])
def process_img(img_path, img_size):
img = cv2.imread(img_path)
img = cv2.resize(img, (img_size, img_size))
img = img.astype(np.float32) / 255.0
img = loader(img)
img = img.unsqueeze(0)
return img第一个是原始图像,第二个是论文提供的图像,第三个是我的代码生成的图像:

可以看出,用我的方法生成的图像与本文提供的图像有很大的不同,而且还存在一些伪影。为何会有这样的结果呢?
回答 1
Stack Overflow用户
回答已采纳
发布于 2021-11-30 12:00:36
您将复数的“真实”/“想象”部分与“振幅”/“相位”表示混淆。
以下是快速指南:
一个复数z可以用实部x和虚部y之和来表示。
z = x + j y
或者,可以将同一复数z表示为具有振幅r和角度phi的旋转矢量。
z = r exp(j phi),r = sqrt(x^2 + y^2)和phi=atan2(x,y)。
这个图像(来自维基百科)直观地解释了这一点:
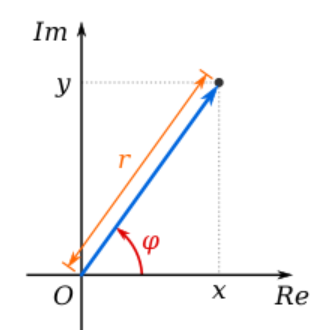
在您的代码中,您替换了“真实”部分,但在论文中,它们建议替换“振幅”。
如果要替换振幅:
const_amp = ... # whatever the constant amplitude you want
new_fft = const_amp * torch.exp(1j * img_fft.angle())
# reconstruct the new image from the modulated Fourier:
img_ifft = torch.fft.ifft2(new_fft, dim=(-2, -1))这样做的结果如下:

页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/70165427
复制相关文章
相似问题

