通过去除不必要的点和叠加形状优化矢量图像
我需要优化一个由bezier线构造的填充形状的矢量图像。输入图像和形状分离时的外观:
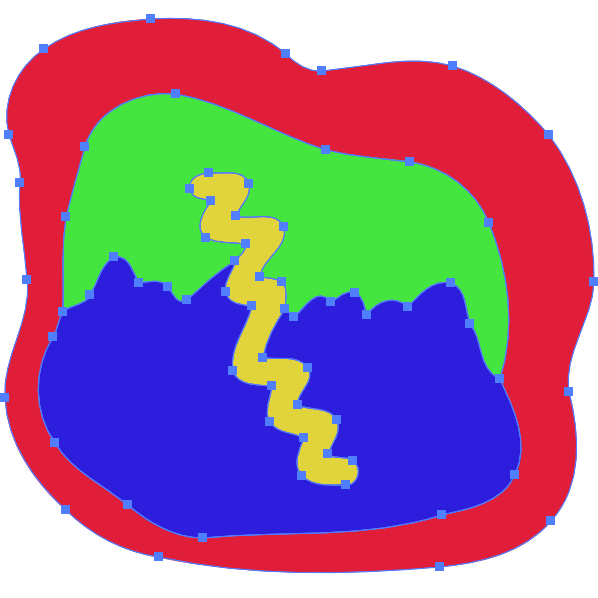

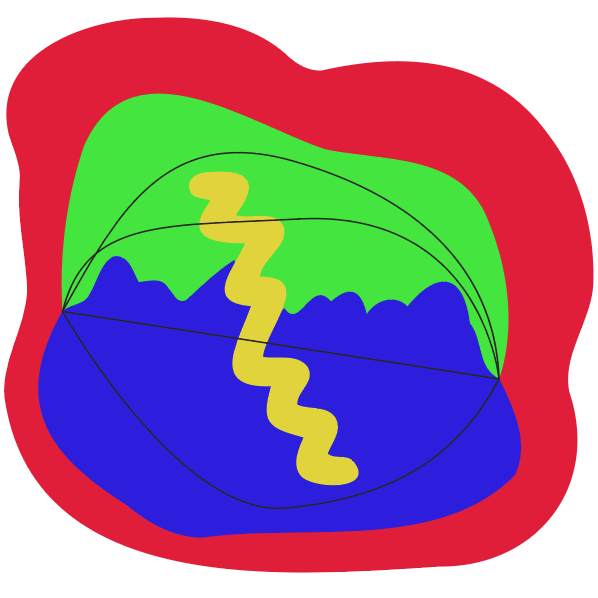
我想优化图像,消除不必要的线条和依靠堆叠的形状,以保持外观,但与更少的顶点。结果形状应该如下所示:

这个问题可能可以分成几个步骤:
- 检测堆叠线。这或多或少是很简单的:沿着一条线计算点,沿着它们找到顶点。如果顶点被堆叠,它就变得琐碎了。
- 通过填充的其他形状区域查找bezier路径。这方面的算法可能已经存在,但我不知道。(,我在这里真的需要帮助。)此外,还不清楚到底是什么形状。也许我应该解决所有的可能性并进行比较。一旦我找到它,它可能会变得更清晰。( welcome.)
是提示/建议)
- 求最优的叠加阶,使顶点数最小。这听起来很痛苦,对像我这样不太热衷于算法的人来说,但这似乎是通过不同的“路径”使顶点的数量最小化,所以这是可以做到的。(如果我是wrong.)
,会纠正我
- 如果一个形状上有一个洞,它可能意味着里面的所有东西都要堆放在上面,所以这是一个单独的简单情况,不需要额外的计算。
总的来说,第二点似乎是最多的(唯一的?)有问题,所以我需要一个正确的方向。
就示例图像而言,如何为可能模糊的绿色形状部分找到bezier路径,使其通过蓝色形状(以及可选的黄色形状),反之亦然,蓝色部分通过绿色形状?我不需要这条路是最短的,我需要它有最小的顶点。
本质上,我需要用最小的顶点数找到这些路径。可以随意地忽略其他的不相关的上下文。
回答 1
Stack Overflow用户
发布于 2021-10-13 01:41:52
我在这里看到了许多困难的问题。一些想法:
直接处理Bézier曲线似乎很困难。我的建议是用多边形来近似它们,或者用一对多边形来逼近它们,一个样本和一个刻字。如果是后者,则需要考虑曲线的二阶导数,以确定它是凸的还是凹的,或者它是否从一条曲线过渡到另一条曲线(如果是的话,在拐点处切它)。
曲线方向可以识别出一个洞,如果边界曲线是定向的,使右手边在形状内,则逆时针曲线表示孔洞。对于简单的Bézier形状,每个包含相应顺时针边界部分的形状都必须堆放在前面。一个简单多边形的顺时针方向/逆时针方向可以通过符号区域进行测试。
曲线简化是一个最短路径问题,但度量不是欧几里德。假设我们知道一些简单多边形的堆叠顺序。给定其中一个多边形P,我们形成了由P的并和与之相交的每一个多边形组成的多边形Q。我们要不断地变形位于q的内部的P的边界部分,以使边的数目最小化。对于每个部分,我们应该能够模拟从一个端点到另一个端点的宽度优先搜索,在隐式无限图中,通过可见性算法。
优化堆叠顺序的让人觉得NP很难。我还没有想出减少的方法;这只是我作为一个获得认证的算法设计者的直觉,我知道一个看似简单的排序问题--反馈集合--是NP难的,而简单的多边形为构造小工具提供了很大的自由。我在实践中的建议是,计算每个多边形的凸包,并声明两个不相交的多边形的顺序并不重要。取此图的补充,并枚举其不包含循环的方向(有有效的算法)。对于每个方向,执行一个拓扑排序,将其扩展到一个总阶,然后对曲线进行相应的优化。如果这仍然太贵的话,我会使用一种遗传算法,特别是带有自然解码器的BRKGA (每个染色体每个形状包含一个数字,按数字对形状进行排序)。
https://stackoverflow.com/questions/69442133
复制相似问题

