每个人到达目的地的最短时间
每个人到达目的地的最短时间
提问于 2021-10-01 15:16:48
我必须设计一个算法来解决一个问题:我们有两组人(A组和B组,A组的人数总是小于或等于B组中的人数),所有的人都站在一条一维线上,每个人都有一个相应的数字来表示它的位置。当计时器开始时,A组的每个人必须在B组中找到一个伴侣,但是B组的人根本不能移动,B组的每个人最多只能有一个伙伴。
假设A组中的人移动1单位/秒,我如何才能为A组中的每个人找到找到伴侣的最短时间?
例如,如果A组中有三人的位置{5,7,8},而B组的位置为{2,3,4,9},则最佳解为3秒,因为最大(5-3,7-4,9-8)=3。
我可以用暴力来解决这个问题,但是有更好的方法解决这个问题吗?
回答 1
Stack Overflow用户
回答已采纳
发布于 2021-10-01 17:13:24
这个问题是编辑距离问题的特例,因此可以使用类似的动态规划解决方案来解决它。对于这种特殊情况,有可能存在一个更快的解决方案。
让A = [a_0, a_1...,a_(m-1)]是我们的m移动人员的(排序)位置,B = [b_0, b_1...,b_(n-1)]是n (排序)目的地,使用m <= n。对于编辑距离类比,允许的操作如下:
- 在
A中插入一个数字(免费),或 - 将
A中的元素|a-a'|替换为|a-a'|。
我们可以在O(n*m)时间解决这个问题(如果需要的话,加上A和B的排序时间)。
我们可以通过成本函数C(i, j)定义动态规划,该函数是仅使用第一个j spots b_0, ... b_(j-1)移动第一个j people a_0, ... a_(i-1)的最小成本。你想要C(m,n)。定义C如下:
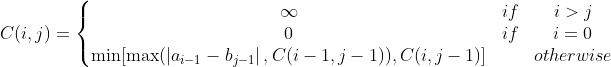
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/69408278
复制相关文章
相似问题

