R中的条件概率
R中的条件概率
提问于 2021-08-19 14:11:05
问题:
一种影响到0.05%男性人群的疾病筛查测试能够在90%的个人实际患有该疾病的病例中识别出这种疾病。然而,这项测试会产生1%的假阳性(当个体没有这种疾病时,给出一个阳性的读数)。在测试阳性的情况下,找出一个人患上这种疾病的可能性。然后,找出一个人患上这种疾病的可能性,因为他的测试是阴性的。
我的错误尝试:
我首先让:·T是一个男人有阳性测试的事件·Tc是一个男人有阴性测试的事件·D是一个男人实际上有疾病的事件·Dc是一个男人没有疾病的事件
因此,我们需要找到P(D=T)和P(D=Tc)。
然后我写了这段代码:
set.seed(110)
sims = 1000
D = rep(0, sims)
Dc = rep(0, sims)
T = rep(0, sims)
Tc = rep(0, sims)
# run the loop
for(i in 1:sims){
# flip to see if we have the disease
flip = runif(1)
# if we got the disease, mark it
if(flip <= .0005){
D[i] = 1
}
# if we have the disease, we need to flip for T and Tc,
if(D[i] == 1){
# flip for S1
flip1 = runif(1)
# see if we got S1
if(flip1 < 1/9){
T[i] = 1
}
# flip for S2
flip2 = runif(1)
# see if we got S1
if(flip2 < 1/10){
Tc[i] = 1
}
}
}
# P(D|T)
mean(D[T == 1])
# P(D|Tc)
mean(D[Tc == 1])我真的很挣扎,所以任何帮助都会很感激!
回答 1
Stack Overflow用户
发布于 2021-08-21 04:08:32
扩展Allan的答案,但将其与Bayes定理联系起来,如果您愿意的话:
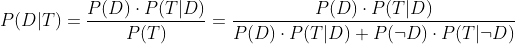
从问题中,你知道(将百分比转化为概率):
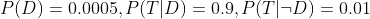
插入:
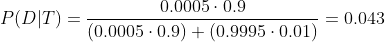
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/68849489
复制相关文章
相似问题

