最大二部匹配图论中的最大流算法为何正确
我读过很多文章,指出用最大流算法可以找到二部图的最大匹配。但是,我们从最大流得到的匹配可能不是最大的,或者匹配没有最大的边。
来自Anti Laaksonen的竞争性方案编制手册的例子:
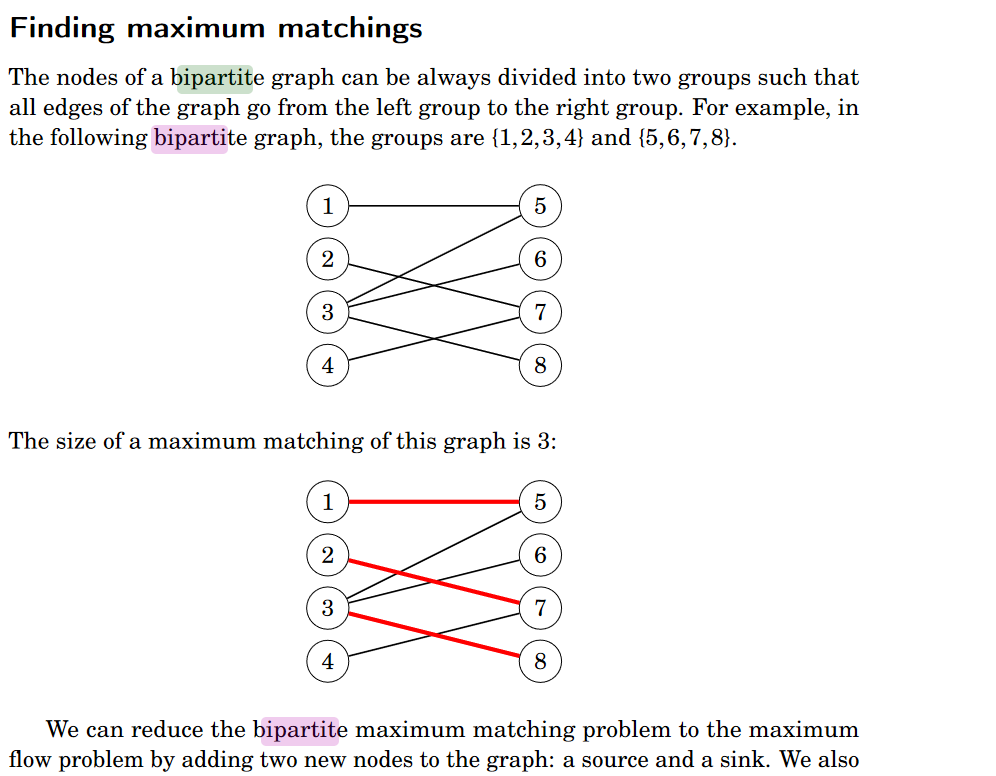
但是,如果我以不同的方式呈现这个图,那么现在的图形是:
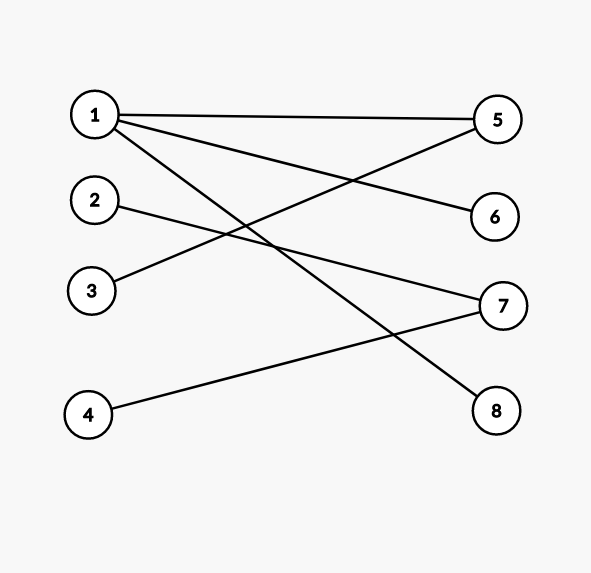
然后,随着最大流量算法的推进,匹配结果为1-5,2-7。
因为1简单地擦除了通向水槽的路径,但是如果它被移到边缘1-6,那么匹配可能是
1
回答 1
Stack Overflow用户
发布于 2021-06-24 17:22:30
在此之前我一直和你在一起
然后,随着最大流量算法的推进,
算法的匹配量为1-5,2--7。
您在这里描述的并不是图中的最大流。我们可以通过发送一个从1到6的流量单位、从2到7的流量单位和从3到5的流量单位来推动更多的流量。
读到你的问题,我认为你最终产生(非最大)流而不是最大流的原因是因为这个说法:
,因为1简单地擦除到接收器的路径。
根据您在这里所描述的,我假设您正在使用类似于福特-富尔克森算法的方法来计算最大流量:找到一个从源到水槽的增强路径,并将流推过它。但是,福特-富尔克森还有第二步:在推动流动越过一个边缘后,我们引入一个剩余的边缘,向相反的方向推进。这使我们有机会“撤销”我们在找到更好道路的情况下作出的决定。
因此,当我们把一个流量单位从1-5推入后,我们再加上一个剩余边,从5返回到1,只有一个单位的容量。这意味着图表现在看起来是这样的:
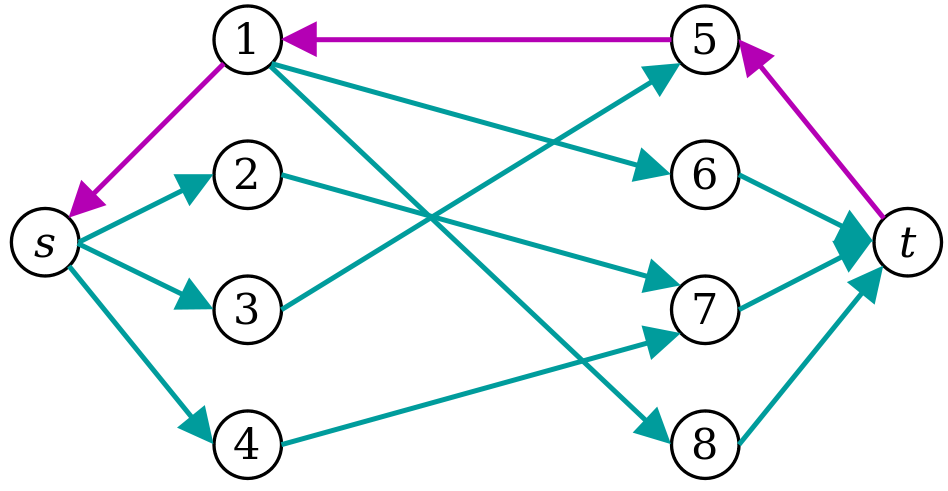
在这里,从s到t的边,紫色的边从t向s的方向流动。
注意,我们可以“撤消”分配1到5的决定,如下所示。在小径上推一个流量单位
s→3→5→1→6→t
为了提供这个流网络:
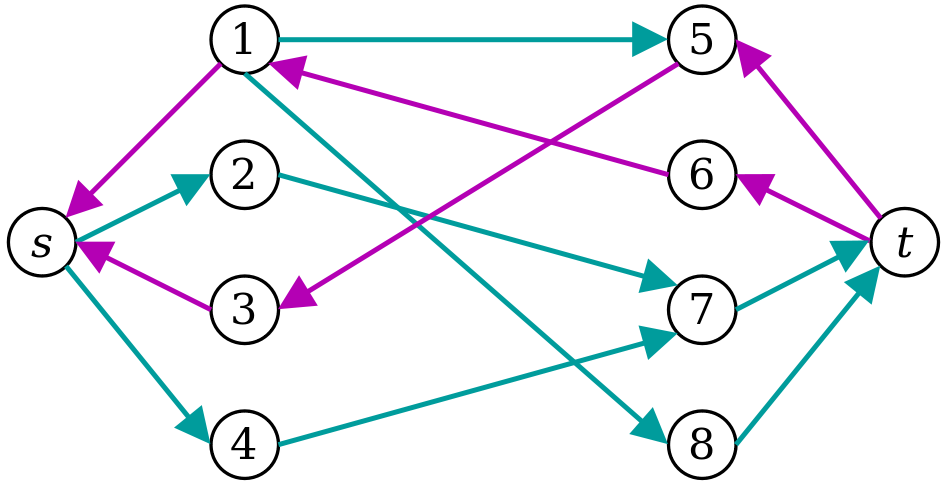
现在,在小路上再推一个单位的流量
s→2→7→t
给出整体匹配值1-6,2-7,3-5,这是一个最大匹配。
https://stackoverflow.com/questions/68118281
复制相似问题

