问何时(最大)堆可以是一个BST？

EN

一开始：

(max)堆是一个完整的二叉树，其中每个节点的值都大于或等于其子节点的值。

BST是一种二叉树，每个节点最多有2个子节点，每个节点的值大于其左子树的所有值，小于其右子树的所有值。

我想到的堆

1. 只有一个值，例如8。因为它没有子树，所以这棵树仅仅是由根组成的。这棵树是完整的，根的值比它的子树的值大，所以它是一个堆。这棵树也是一个没有孩子的BST树。所以有一个堆，它也是BST.

。

，

1. ，这当然是假的。设最大堆为：

​

​

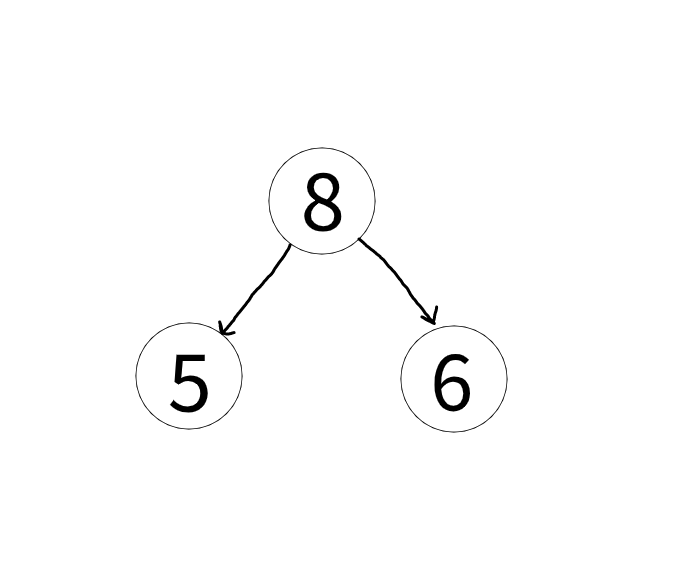
当然，这是一个最大的堆，但不是BST，因为6位于8的右边。

1. 我认为这是正确的，正如我在(1)

中所解释的那样

1. 最多可以有两个节点，这意味着我们可以有0、1或2个节点。

如果我们有0节点，它就会保持。

如果我们有一个节点，它也成立，我们证明了。

如果我们有两个节点，它也会保持。让最大堆有两个节点.要使其成为max-堆，它必须是一棵完整的树，因此根据定义，第二个节点应该放在第一个节点(根)的左侧。根据最大堆的定义，第二个节点还包含小于第一个节点(根)的值。这也是具有两个节点的BST树。所以这是正确的。

如果有什么不正确的地方，请指出。谢谢！)

这太棘手了！让我们逐一探讨所有的选择。

从你问题的选项来看：

堆永远不可能是BST

不对。因为有一两个元素的堆也可以是有效的BST。(见第三选项中的示例)

堆总是BST。

不对。从您的例子中可以清楚地看到，堆有时不能保存BST的属性，特别是Max-Heap。

如果堆中只有一个节点(根)，则堆可以是BST。

不对。因为一棵有两个孩子的树也能拥有BST的属性。

例子-

              3
               \ 
                5 

上面的节点结构是BST，同时也是一个Min.

堆可以是BST当且仅当它有最多2个节点时。

你猜怎么着！也错了！因为单个节点可以是有效的BST以及Max/Min。