Python中的快速傅里叶图
Python中的快速傅里叶图
提问于 2021-01-03 16:06:22
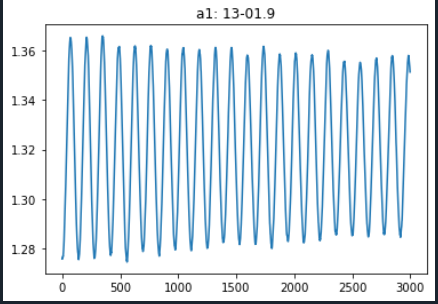
我有一个时域振动数据,并希望将其转换为频域与fft。然而,FFT的图只显示了一个大的峰值在零,而没有其他。
这是我的振动数据:https://pastebin.com/7RK57kJW
我的代码:
import numpy as np
import matplotlib.pyplot as plt
t = np.arange(3000)
a1_fft= np.fft.fft(a1, axis=0)
freq = np.fft.fftfreq(t.shape[-1])
plt.plot(freq, a1_fft)我的FFT图:
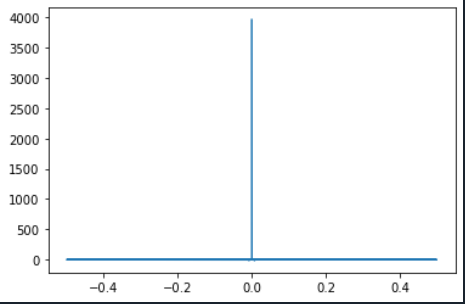
我在这里做错什么了?我很确定我的数据是一致的,在其他情况下,fft也会引发类似的问题。
回答 2
Stack Overflow用户
回答已采纳
发布于 2021-01-03 18:41:49
快速傅立叶变换的回收箱对应于0, df, 2df, 3df, ..., F-2df, F-df的频率,其中df是由垃圾箱数决定的,F是每个垃圾箱的一个周期。
注意开始处的零频率。这就是所谓的直流偏移。这是你数据的平均值。在你显示的数据中,平均值是1.32,而正弦波的振幅在0.04左右。难怪你看不到一个比直流电项小33倍的峰值。
有一些常见的方法可以使数据可视化,从而帮助您解决这个问题。一种常见的方法是保持DC偏移量,但至少对y轴使用日志刻度:
plt.semilogy(freq, a1_fft)或
plt.loglog(freq, a1_fft)另一件事,你可以做的是放大的底部1/33左右的情节。您可以手动完成此操作,或者通过调整显示的Y轴的跨度:
p = np.abs(a1_fft[1:]).max() * [-1.1, 1.1]
plt.ylim(p)如果您正在绘制绝对值,请使用
p = np.abs(a1_fft[1:]).max() * [-0.1, 1.1]另一种方法是删除直流偏移量。一种比@J. Schmidt建议的更优雅的方法是不显示DC术语:
plt.plot(freq[1:], a1_fft[1:])或仅适用于正频率:
n = freq.size
plt.plot(freq[1:n//2], a1_fft[1:n//2])在n // 2的截止值只是近似的。正确的截止取决于FFT是有偶数元素还是奇数元素。对于偶数,中间仓的实际能量来自光谱的两边,并且经常得到特殊处理。
Stack Overflow用户
发布于 2021-01-03 17:36:57
峰值在0是直流增益,这是非常高,因为你没有正常化你的数据。另外,傅里叶变换是一个复数,你应该分别画出绝对值和相位。在这段代码中,我只画出了正频率:
import numpy as np
import matplotlib.pyplot as plt
#Import data
a1 = np.loadtxt('a1.txt')
plt.plot(a1)
#Normalize a1
a1 -= np.mean(a1)
#Your code
t = np.arange(3000)
a1_fft= np.fft.fft(a1, axis=0)
freq = np.fft.fftfreq(t.shape[-1])
#Only plot positive frequencies
plt.figure()
plt.plot(freq[freq>=0], np.abs(a1_fft)[freq>=0])页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/65551946
复制相关文章
相似问题

