从均匀随机数中获得符合卡方分布的直方图的r码
我在我的教科书 (用日语写的)中有一个代码,用来生成一个不受均匀分布的3自由度的卡方分布。我对此进行了改进,并创建了一个代码来获得一个直方图,该直方图遵循具有4自由度的卡方分布。这与R的分布函数非常一致,所以我认为它可能正确工作(参见下面的Box1 )。
我试图进一步完善Box1 1的代码,以获得一个带有指定自由度的卡方分布的直方图,但它不适用于许多错误。(见Box2)
我的问题:
Box2 2从均匀分布生成卡方分布的代码不能很好地工作。 请帮助我修复Box2 2代码中的错误。
“y<-ifelse(x<0.2,1,ifelse(x<0.4,2,ifelse(x<0.6,3,ifelse(x<0.8,4,5)”的泛化可能在框2中不起作用。
Box1 1:获取一个直方图的代码,该直方图遵循带有4个自由度(可能正确工作的)的卡方分布。
ite <- 10000
sc <- numeric(ite) #★1
A<- c(20,20,20,20,20) #★2
for(i in 1:ite){
s<- runif(sum(A)*5) #★3
y<-ifelse(s<0.2,1,ifelse(s<0.4,2,ifelse(s<0.6,3,ifelse(s<0.8,4,5)))) #★4
z1 <- table(y)
z2 <- A*5
z3 <- (z1-z2)^2 /z2
sc[i] <- sum(z3)
}
hist(sc,ylim=c(0,0.35),breaks="Scott",freq=F)
curve(dchisq(x,4),add=T)框1的代码是根据以下事实设计的;如果将500=sum(A)*5均匀随机数划分为五个相同大小的房间,则进入每个房间的数的期望值为100。这里,第一个房间,第二个房间,.和第五个房间是由0≦x<0.2,0.2≦x<0.4,.我们可以从下面框‘1中表(Y)的输出中看到这一点。当然,方框1的和(Y)总是得到500的结果。
Box1的逻辑用于在Box1 1码上生成均匀随机数(X)逐步(Y)
A<- c(20,20,20,20,20)
s<- runif(sum(A)*5) #★3
y<-ifelse(s<0.2,1,ifelse(s<0.4,2,ifelse(s<0.6,3,ifelse(s<0.8,4,5))))
table(y)
sum(table(y))Box2 2:按照自由度n(有许多错误)的卡方分布获得直方图的代码
chiq_dist_n<-function(numb,itr){
A<-numeric(numb) #★2
aa<-numeric(numb) #★4-1
for(i in 1:numb){
A[i]=20
} #★2
ntot=sum(A)
for(i in 1:numb){
if (i ==1){aa[i]= A[i]/ntot
}else{
aa[i]=aa[i-1]+(A[i]/ntot)
}
} #★4-2
sc<-numeric(itr) #★1
y<-numeric(ntot*numb) #★4-3
for(i in 1:itr){
x<-runif(ntot*numb)
for(k in 1:ntot*numb){
for(j in 1:numb){
if (x[k]<aa[numb-j+1]) {
y[k]<-j
} else {}
}
}#★3
z1<-table(y)
z2<-A*ntot
z3<-(z1-z2)^2/z2
sum(z3)
sc[i]<-sum(z3)
}
return(sc)
}
hist(chiq_dist(10,1000),ylim=c(0,0.35),breaks="Scott",freq=F)Box2代码中生成y的部分被裁剪到Box2 2‘中。如果你看一下Box2 2‘的表(Y),你会发现太多的易是零。我希望方框2‘中表(Y)的输出与框1’中表(Y)的输出大致相同。
Box2的逻辑用于在Box2 2码上生成均匀随机数(X)逐步(Y)
A<- c(20,20,20,20,20)
ntot=sum(A)
numb=length(A)
aa<-numeric(numb)
for(i in 1:numb){
if (i ==1){aa[i]= A[i]/ntot
}else{
aa[i]=aa[i-1]+(A[i]/ntot)
}
} #★4-2
y<-numeric(ntot*numb)
x<-runif(ntot*numb)
for(k in 1:ntot*numb){
for(j in 1:numb){
if (x[k]<aa[numb-j+1]) {
y[k]<-j
} else {}
}
}#★3
table(y)回答 1
Stack Overflow用户
发布于 2020-11-01 10:14:27
您不需要ifelse来破坏随机的均匀分布,您只需使用cut()并指定中断的次数,例如:
set.seed(111)
v = runif(10)
[1] 0.59298128 0.72648112 0.37042200 0.51492383 0.37766322 0.41833733
[7] 0.01065785 0.53229524 0.43216062 0.09368152
cut(v,breaks=seq(0,1,length.out=numb+2),labels=1:5)
[1] 3 4 2 3 2 3 1 3 3 1我不太确定A或者它是做什么的,但是为了模拟chisquare,我想您应该做一个标签1:(df+1)的随机样本,其中df是自由度。如果我们将样本数固定在500个,那么我们就知道每次中断的预期值是500/(df+1)。
所以在不改变太多代码的情况下。
chiq_dist_n<-function(numb,ite){
sc <- numeric(ite)
for(i in 1:ite){
x<- runif(500) #★3
y<- cut(x,breaks=seq(0,1,length.out=numb+2),labels=1:(numb+1))
z1 <- table(y)
z2 <- length(x)/(numb+1)
z3 <- (z1-z2)^2 /z2
sc[i] <- sum(z3)
}
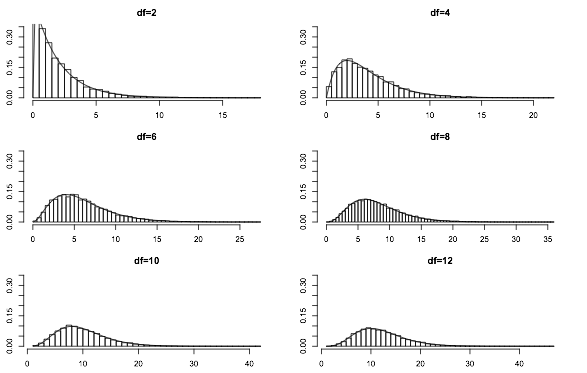
hist(sc,ylim=c(0,0.35),breaks="Scott",freq=F,main=paste0("df=",numb))
curve(dchisq(x,numb),add=T)
}我们尝试从4到9:
par(mfrow=c(3,2))
par(mar=c(2.5,2.5,2.5,2.5))
for(i in seq(2,12,2)){
chiq_dist_n(i,10000)
}
https://stackoverflow.com/questions/64630051
复制相似问题

