如何使用__builtin_ctz加速二进制GCD算法?
clang和GCC有一个int __builtin_ctz(unsigned)函数。这将计数整数中的尾随零。维基百科关于这一系列功能的文章提到可以使用__builtin_ctz加速二进制GCD算法,但我不明白如何实现。
二进制GCD的样本实现如下所示:
unsigned int gcd(unsigned int u, unsigned int v)
{
// simple cases (termination)
if (u == v)
return u;
if (u == 0)
return v;
if (v == 0)
return u;
// look for factors of 2
if (~u & 1) // u is even
if (v & 1) // v is odd
return gcd(u >> 1, v);
else // both u and v are even
return gcd(u >> 1, v >> 1) << 1;
if (~v & 1) // u is odd, v is even
return gcd(u, v >> 1);
// reduce larger argument
if (u > v)
return gcd(u - v, v);
return gcd(v - u, u);
}我怀疑我可以使用__builtin_ctz,如下所示:
constexpr unsigned int gcd(unsigned int u, unsigned int v)
{
// simplified first three ifs
if (u == v || u == 0 || v == 0)
return u | v;
unsigned ushift = __builtin_ctz(u);
u >>= ushift;
unsigned vshift = __builtin_ctz(v);
v >>= vshift;
// Note sure if max is the right approach here.
// In the if-else block you can see both arguments being rshifted
// and the result being leftshifted only once.
// I expected to recreate this behavior using max.
unsigned maxshift = std::max(ushift, vshift);
// The only case which was not handled in the if-else block before was
// the odd/odd case.
// We can detect this case using the maximum shift.
if (maxshift != 0) {
return gcd(u, v) << maxshift;
}
return (u > v) ? gcd(u - v, v) : gcd(v - u, u);
}
int main() {
constexpr unsigned result = gcd(5, 3);
return result;
}不幸的是,这还不起作用。程序的结果是4,当它应该是1。那么我做错了什么?我怎么才能在这里正确使用__builtin_ctz?到目前为止,在GodBolt上查看我的代码。
回答 2
Stack Overflow用户
发布于 2020-08-26 23:40:40
下面是我在评论中的迭代实现
虽然尾递归算法通常是优雅的,但迭代实现在实践中几乎总是更快。(在非常简单的情况下,现代编译器实际上可以执行这种转换。)
unsigned ugcd (unsigned u, unsigned v)
{
unsigned t = u | v;
if (u == 0 || v == 0)
return t; /* return (v) or (u), resp. */
int g = __builtin_ctz(t);
while (u != 0)
{
u >>= __builtin_ctz(u);
v >>= __builtin_ctz(v);
if (u >= v)
u = (u - v) / 2;
else
v = (v - u) / 2;
}
return (v << g); /* scale by common factor. */
}如前所述,|u - v| / 2步骤通常被实现为非常有效、无条件的右移,例如,|u - v| / 2被(2)除以--因为(u)、(v)都是奇数,因此|u - v|必须是偶数。
严格来说,这并不是必要的,因为“奇怪”步骤:u >>= __builtin_clz(u);将在下一次迭代中有效地执行此操作。
假设tzcnt,中的(u)或(v)具有“随机”比特分布,则(n)尾随零点的概率为~ (1/(2^n))。本指令是对bsf,的改进,即__builtin_clz在Haswell,IIRC之前的实现。
Stack Overflow用户
发布于 2020-08-26 20:26:10
感谢乐于助人的评论员,我发现了一个关键的错误:我应该使用min而不是max。
这是最后的解决办法:
#include <algorithm>
constexpr unsigned gcd(unsigned u, unsigned v)
{
if (u == v || u == 0 || v == 0)
return u | v;
// effectively compute min(ctz(u), ctz(v))
unsigned shift = __builtin_ctz(u | v);
u >>= __builtin_ctz(u);
v >>= __builtin_ctz(v);
const auto &[min, max] = std::minmax(u, v);
return gcd(max - min, min) << shift;
}
int main() {
constexpr unsigned g = gcd(25, 15); // g = 5
return g;
}这个解决方案也很好,几乎没有分支的编译输出。
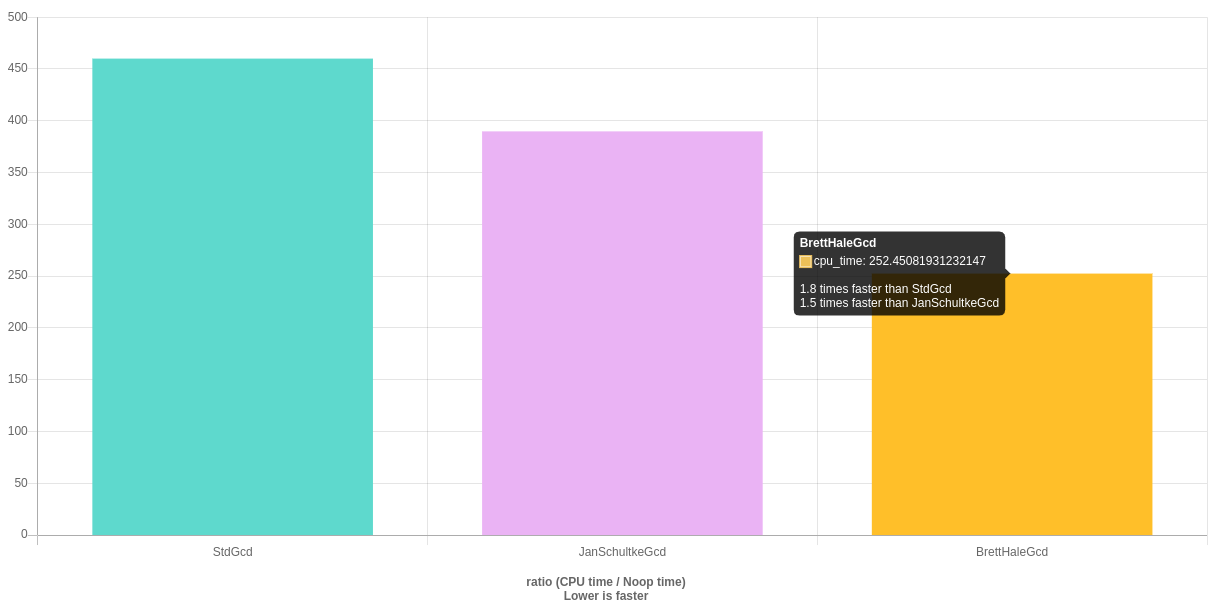
以下是到目前为止所有答案的一些基准结果 (我们实际上击败了std::gcd):
https://stackoverflow.com/questions/63604914
复制相似问题

