来自特定似然函数的最大似然估计的r码
我一直试图从纸中的日志似然函数(第609页方程9)中生成用于最大似然估计的R码。本文作者用MATLAB对其进行了估计,但我对此并不熟悉。所以我试图在R中生成代码。
以下是本文中日志似然函数的快照:

,其中
r:二进制位决定(0或1)指示受侵扰的植物检测(1)或不(0)。
e:检查效率。这是众所周知的。
n:样本量
总体目标是根据对受侵染植物的存在和不存在的二元判断来估计植物侵染率(γ:γ)和epsilon (e),而不是使用检测到的受侵染植物。因此,该函数只包含了侵染植物检测和样本大小的二进制信息。由于epsilon (e)已知或固定,实际目标是估计人口中的伽马(γ)。
另一个目的是将上述估计的侵染率与另一篇论文 (第6页)中超几何抽样公式中的估计侵染率进行比较。公式是:

这个公式产生了所需的样本大小,以便在给定侵染率的情况下,以选定的概率(例如,95)来检测受侵扰的植物。例如:
# Sample size calculation function
fosgate.sample1 <- function(box, p, ci){ # Note: box represent total plant number
ninf <- p*box
sample.size <- round(((1-(1-ci)^(1/ninf))*(box-(ninf-1)/2)))
#sample.size <- ceiling(((1-(1-ci)^(1/ninf))*(box-(ninf-1)/2)))
sample.size
}
fosgate.sample1(box=100, p = .05, ci = .95) # where box: population or total plants, p: infestation rate, and ci: probability of detection
## 44其思想是,如果提供样本大小(例如44)和二进制决策数据,则可以使用对数似然函数来估计侵扰率,并且该速率可能接近预期速率(例如,.05)。最后,我想比较从上面的对数似然函数和样本大小计算公式(第二)中的D/N估计的植物侵染率(伽马:),或者在下面的样本编码中比较p。
我为上面描述的日志似然生成了R代码.
### MLE with stat4
library(stats4)
# Log-likelihood function
plant.inf.lik <- function(inf.rate){
logl <- suppressWarnings(
sum((1-insp.result)*n*log(1-inf.rate) +
insp.result*log(1-(1-inf.rate)^n))
)
return(-logl)
}使用样本量函数(即fosgate.sample1),为函数中的总工厂(或箱)和预期检测率(p)的各种情况生成样本大小。由于我也对估计的植物侵染率的误差/置信范围感兴趣,所以我使用自举法来计算估计值的范围(我不确定这是否适当/可接受)。下面是我生成的最后代码:
### MLE and CI with bootstrapping with multiple scenarios
plant <- c(100, 500, 1000, 5000, 10000, 100000) # Total plant number
ir <- seq(.01, .2, by = .01) # Plant infestation rate
df.result <- data.frame(expand.grid(plant=plant, inf.rate = ir))
df.result$sample.size <- fosgate.sample1(box=df.result$plant, p=df.result$inf.rate, ci=.95) # Sample size
df.result$insp.result <- 1000 # Shipment number (can be replaced with random integers)
df.result <- df.result[order(df.result$plant, df.result$inf.rate, df.result$sample.size), ]
rownames(df.result) <- 1:nrow(df.result)
df.result$est.mean <- 0
#df.result$est.median <- 0
df.result$est.lower.ci <- 0
df.result$est.upper.ci <- 0
df.result$nsim <- 0
str(df.result)
head(df.result)
# Looping
est <- rep(NA, 1000)
for(j in 1:nrow(df.result)){
for(i in 1:1000){
insp.result <- sample(c(rep(1, df.result$insp.result[j]-df.result$insp.result[j]*df.result$inf.rate[j]),
rep(0, df.result$insp.result[j]*df.result$inf.rate[j])))
ir <- df.result$inf.rate[j]
n <- df.result$sample.size[j]
insp.result <- sample(insp.result, replace = TRUE)
est[i] <- mle(plant.inf.lik, start = list(inf.rate = ir*.9), method = "BFGS", nobs = length(insp.result))@coef
df.result$est.mean[j] <- mean(est, na.rm = TRUE)
# df.result$est.median[j] <- median(est, na.rm = TRUE)
df.result$est.lower.ci[j] <- quantile(est, prob = .025, na.rm = TRUE)
df.result$est.upper.ci[j] <- quantile(est, prob = .975, na.rm = TRUE)
df.result$nsim[j] <- length(est)
}
}
# Significance test result
sig <- ifelse(df.result$inf.rate >= df.result$est.lower.ci & df.result$inf.rate <= df.result$est.upper.ci, "no sig", "sig")
table(sig)
# Plot
library(ggplot2)
library(reshape2)
df.result$num <- ave(df.result$inf.rate, df.result$plant, FUN=seq_along)
df.result.m <- melt(df.result, id.vars=c("plant", "sample.size", "insp.result", "est.lower.ci", "est.upper.ci", "nsim", "num"))
df.result.m$est.lower.ci <- ifelse(df.result.m$variable == "inf.rate", NA, df.result.m$est.lower.ci)
df.result.m$est.upper.ci <- ifelse(df.result.m$variable == "inf.rate", NA, df.result.m$est.upper.ci)
str(df.result.m)
ggplot(data = df.result.m, aes(x = num, y = value, group=variable, color=variable, shape=variable))+
geom_point()+
geom_errorbar(aes(ymin = est.lower.ci, ymax = est.upper.ci), width=.5)+
scale_y_continuous(breaks = seq(0, .2, .02))+
xlab("Index")+
ylab("Plant infestation rate")+
facet_wrap(~plant, ncol = 3)当我运行代码时,我能够获得结果并比较估计(est.mean)和预期(inf.rate)的侵扰率,如下图所示。
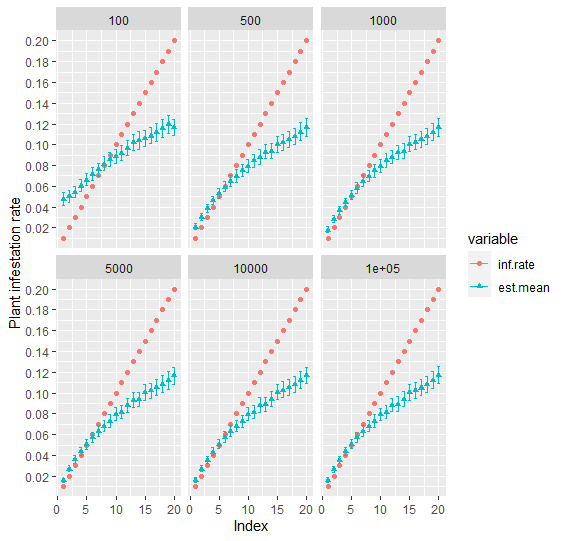
如果结果是正确的,绘图表明,估计似乎很好,但对更大的侵扰率。
此外,我总是收到没有"suppressWarnings“函数的警告消息,并在下面偶尔收到错误消息。我不知道怎么修理它们。
## Warning messages
## 29: In log(1 - (1 - inf.rate)^n) : NaNs produced
## 30: In log(1 - inf.rate) : NaNs produced
## Error message (occasionally)
## Error in solve.default(oout$hessian) :
## Lapack routine dgesv: system is exactly singular: U[1,1] = 0我的问题是:
- R函数(plant.inf.lik)是否适用于对数似然函数的最大似然估计?
- 我应该处理警告和错误消息吗?如果是,怎么做?再说一次,我不知道该怎么修理.
- 是引导(重采样)吗?适合于估计CI范围和/或标准误差的方法?
我发现此链接对于替代方法很有用。虽然我仍然在这两种方法一起工作,但结果似乎不一样(可能是下面的问题)。
任何建议都将不胜感激。
回答 1
Stack Overflow用户
发布于 2020-07-27 19:43:27
关于您关于估计CI范围的最后一个问题,有三种常用的ML估计方法:
- 从倒Hessian矩阵估计方差。
- 方差的加刀估计(如果Hessian是用数值估计的,则更简单和更稳定,但在计算上比较昂贵)
- 引导CIs (计算上最昂贵的方法)。
对于引导CIs,您不需要自己实现它们(例如,偏倚校正可能很棘手),但是可以依赖R库引导。
顺便提一句,我在两年前为所有三种方法编写了一个带有R代码的摘要:置信区间的构造 (参见第5节)。例如,对于使用Hessian矩阵的方法,大纲如下:
lnL <- function(theta1, theta2, ...) {
# definition of the negative (!)
# log-likelihood function...
}
# starting values for the optimization
theta0 <- c(start1, start2, ...)
# optimization
p <- optim(theta0, lnL, hessian=TRUE)
if (p$convergence == 0) {
theta <- p$par
covmat <- solve(p$hessian)
sigma <- sqrt(diag(covmat))
}来自stats4的函数mle已经封装了凸矩阵估计,并在vcov中重新运行。然而,在我尝试过的实际用例中(配对比较模型),这种估计是相当不稳定的,我转而使用了刀法。
https://stackoverflow.com/questions/63117891
复制相似问题

