问为什么加性噪声在微分隐私中需要用灵敏度来校准？

EN

可以直观地理解这一点的一种方法是，想象一个函数返回两个值中的任何一个，例如0和a作为实的a。

进一步假设我们有一个加性噪声机制，这样我们在真实的线上得到两个概率分布，就像您所附链接中的图像一样(这是上面使用a=1的设置的一个例子)：

​

​

在纯DP中，我们感兴趣的是计算这些分布在整个实际线上的比率的最大值。正如链接中的计算所示，这个比率在任何地方都被e和epsilon的幂所限制。

现在，设想将这些分布的中心进一步分开，比如将红色分布移到右边(IE，增加a)。很明显，这将减少红色分布在0上的概率质量，这是这个比率的最大值。因此，这些分布在0处的比率会增加--一个常数(蓝色分布位置在0上的质量)除以一个较小的数。

我们可以将比例降下来的一种方法是“肥肥”出分布。这将对应于将分布的峰值移到更低的位置，并将质量分散到更宽的区域(因为它们必须整合到1，这两件事必然耦合到像Laplace这样的分布中)。在数学上，我们将通过增加Laplace分布的方差(在参数化这里中增加b)来实现这一点，它的作用是降低蓝色分布在0的峰值，并在0处提高红色分布位置的质量，从而降低它们之间的比值(较小的分子和较大的分母)。

如果执行计算，您将发现方差参数b与函数f的灵敏度之间的关系实际上是线性的，也就是说，将b设为

​

​

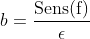
将此比率的最大值修正为

​

​

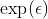
这正是纯差别隐私的定义。

如果你添加任意数量的随机噪声，你就会得到随机数据。当然，它保留了隐私，但同时也破坏了数据中的任何真实价值。您添加的噪声需要与现有分布相匹配，以便在不破坏数据值的情况下保护隐私。校准步骤就是这么做的。