Runge-Kutta python的Lorenz吸引子
Runge-Kutta python的Lorenz吸引子
提问于 2020-06-14 19:24:00
- 你好,我要编写python函数,用Runge-Kutta 2 2cond级数求解Lorenz微分方程。
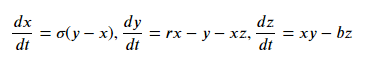
sigma=10,r=28和b=8/3
初始条件为(x,y,z)=(0,1,0)
这是我编写的代码,但是它抛出了一个错误,说明在double_scalars中遇到了溢出,我不知道程序有什么问题
from pylab import *
def runge_4(r0,a,b,n,f1,f2,f3):
def f(r,t):
x=r[0]
y=r[1]
z=r[2]
fx=f1(x,y,z,t)
fy=f2(x,y,z,t)
fz=f3(x,y,z,t)
return array([fx,fy,fz],float)
h=(b-a)/n
lista_t=arange(a,b,h)
print(lista_t)
X,Y,Z=[],[],[]
for t in lista_t:
k1=h*f(r0,t)
print("k1=",k1)
k2=h*f(r0+0.5*k1,t+0.5*h)
print("k2=",k2)
k3=h*f(r0+0.5*k2,t+0.5*h)
print("k3=",k3)
k4=h*f(r0+k3,t+h)
print("k4=",k4)
r0+=(k1+2*k2+2*k3+k4)/float(6)
print(r0)
X.append(r0[0])
Y.append(r0[1])
Z.append(r0[2])
return array([X,Y,Z])
def f1(x,y,z,t):
return 10*(y-x)
def f2(x,y,z,t):
return 28*x-y-x*z
def f3(x,y,z,t):
return x*y-(8.0/3.0)*z
#and I run it
r0=[1,1,1]
runge_4(r0,1,50,20,f1,f2,f3)回答 3
Stack Overflow用户
回答已采纳
发布于 2020-06-14 19:46:28
数值求解微分方程是很有挑战性的。如果您选择的步长太高,解决方案会累积大量错误,甚至会变得不稳定,就像您的情况一样。
要么您应该大幅减少步骤大小(h),要么只使用scipy提供的自适应Runge方法。
from numpy import array, linspace
from scipy.integrate import solve_ivp
import pylab
from mpl_toolkits import mplot3d
def func(t, r):
x, y, z = r
fx = 10 * (y - x)
fy = 28 * x - y - x * z
fz = x * y - (8.0 / 3.0) * z
return array([fx, fy, fz], float)
# and I run it
r0 = [0, 1, 0]
sol = solve_ivp(func, [0, 50], r0, t_eval=linspace(0, 50, 5000))
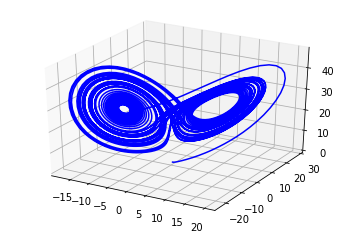
# and plot it
fig = pylab.figure()
ax = pylab.axes(projection="3d")
ax.plot3D(sol.y[0,:], sol.y[1,:], sol.y[2,:], 'blue')
pylab.show()该求解器采用四阶和五阶龙格库塔组合,通过调整步长来控制它们之间的偏差。请参阅此处的更多使用文档:ivp.html
Stack Overflow用户
发布于 2020-06-15 08:02:47
您使用的步长为h=2.5。
对于RK4来说,给出Lipschitz常数L的有用步长在L*h=1e-3到0.1的范围内,人们可能会在L*h=2.5上得到一些正确的结果。在此基础上,该方法变得混乱,与底层ODE的任何相似之处都将消失。
Lorenz系统的Lipschitz常数约为L=50,参见混沌与ODE解的连续依赖性,因此绝对需要h<0.05,h=0.002更好,h=2e-5给出了该数值方法的最佳数值结果。
Stack Overflow用户
发布于 2020-06-14 19:56:33
它可以与除以零相关,或者当超出类型的限制时(浮点类型)。
要确定何时何地发生这种情况,您可以设置numpy.seterr('raise'),它将引发一个异常,这样您就可以调试并查看它正在发生的情况。看来你的算法不一样了。
在这里您可以了解如何使用numpy.seterr
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/62377219
复制相关文章
相似问题

