R中正态分布随机变量的平均模拟
R中正态分布随机变量的平均模拟
提问于 2020-06-05 08:00:20
我试图在R中模拟一些数据,以检查我的手工计算,在一个简单的模型中,方差是如何变化的,这个模型涉及一个正态分布的随机变量序列的平均值。然而,我发现我得到的结果不仅与我的手工计算不一致,而且相互矛盾。很明显,我做错了什么,但我很难把问题隔离开来。
从概念上讲,该模型包括两个步骤:第一步,存储变量;第二步,使用存储的变量生成输出。然后将输出存储为一个新变量,对未来的输出做出贡献,等等。我假设存储是有噪声的(也就是说,存储的是一个随机变量而不是常数),但是在输出生产中没有添加进一步的噪声,这只需要对现有存储变量进行平均处理。因此,我的模型涉及以下步骤,其中V_i是存储在第一步的变量,O_i是第一步的输出:
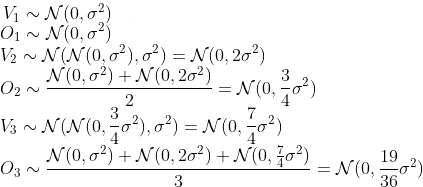
诸若此类。
我试着用两种方法来模拟这一点:第一,
nSamples <- 100000
o1 <- rnorm(nSamples) # First output
o2 <- rowMeans(cbind(rnorm(nSamples, mean=o1),rnorm(nSamples))) # Second output, averaged from first two stored variables.
o3 <- rowMeans(cbind(rnorm(nSamples, mean=o2),rnorm(nSamples, mean=o1),rnorm(nSamples))) # Third output, averaged from first three stored variables.这给了我
var(o1) # Approximately 1, as per my manual calculations.
var(o2) # Approximately .75, as per my manual calculations.
var(o3) # Approximately .64, where my manual calculations give 19/36 or approximately .528.起初,我相信代码,并认为我的计算是错误的。然后,我尝试了以下替代代码,这些代码更显式地遵循了我手动使用的步骤:
nSamples <- 100000
initialValue <- 0
v1 <- rnorm(nSamples, initialValue)
o1 <- v1
v2 <- rnorm(nSamples, o1)
o2 <- rowMeans(cbind(v1, v2))
v3 <- rnorm(nSamples, o2)
o3 <- rowMeans(cbind(v1, v2, v3))这给了我
var(o1) # Approximately 1, as per my calculations.
var(o2) # Approximately 1.25, where my calculations give .75.
var(o3) # Approximately 1.36, where my calculations give approximately .528.因此,显然我在使用这三种方法中至少两种方法时做错了什么,但是我在隔离问题的根源方面遇到了困难。是什么让我的代码与我所期望的不同呢?这两个代码示例之间的差异是什么?这两个代码示例导致方差在一个中减小,另一个中增加?
回答 1
Stack Overflow用户
回答已采纳
发布于 2020-06-05 17:54:40
正确的计算是第一次,在平均时,您正在生成正常随机变量的新实现,而不是使用在前一步中生成的实现。
实际上,O2的分布假定被平均的两个正态随机变量是相互独立的。
在第二次计算中,这是不正确的,因为平均v1和v2并不独立,因为两者都依赖于o1。这就是为什么在第二种情况下,差异更大的原因。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/62210714
复制相关文章
相似问题

