火炬中的弱优化器
考虑一个简单的线拟合a * x + b = x,其中a,b是优化的参数,x是所给出的观测向量
import torch
X = torch.randn(1000,1,1)可以立即看到,确切的解决方案是a=1,b=0,对于任何x,它可以很容易地找到,就像:
import numpy as np
np.polyfit(X.numpy().flatten(), X.numpy().flatten(), 1)我现在试图通过梯度下降的方法在PyTorch中找到这个解,这里的均方误差被作为一个优化准则。
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
from torch.optim import Adam, SGD, Adagrad, ASGD
X = torch.randn(1000,1,1) # Sample data
class SimpleNet(nn.Module): # Trivial neural network containing two weights
def __init__(self):
super(SimpleNet, self).__init__()
self.f1 = nn.Linear(1,1)
def forward(self, x):
x = self.f1(x)
return x
# Testing default setting of 3 basic optimizers
K = 500
net = SimpleNet()
optimizer = Adam(params=net.parameters())
Adam_losses = []
optimizer.zero_grad() # zero the gradient buffers
for k in range(K):
for b in range(1): # single batch
loss = torch.mean((net.forward(X[b,:,:]) - X[b,:, :])**2)
loss.backward()
optimizer.step()
Adam_losses.append(float(loss.detach()))
net = SimpleNet()
optimizer = SGD(params=net.parameters(), lr=0.0001)
SGD_losses = []
optimizer.zero_grad() # zero the gradient buffers
for k in range(K):
for b in range(1): # single batch
loss = torch.mean((net.forward(X[b,:,:]) - X[b,:, :])**2)
loss.backward()
optimizer.step()
SGD_losses.append(float(loss.detach()))
net = SimpleNet()
optimizer = Adagrad(params=net.parameters())
Adagrad_losses = []
optimizer.zero_grad() # zero the gradient buffers
for k in range(K):
for b in range(1): # single batch
loss = torch.mean((net.forward(X[b,:,:]) - X[b,:, :])**2)
loss.backward()
optimizer.step()
Adagrad_losses.append(float(loss.detach()))从损失演变的角度来看,培训的进展可以显示为
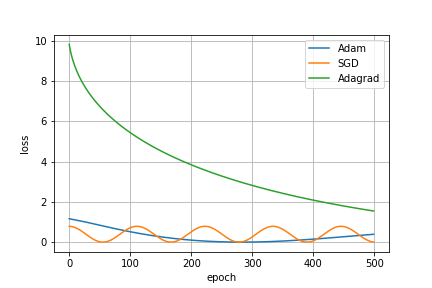
令我惊讶的是,在默认设置中,算法的收敛速度非常慢。因此,我有两个问题:
( 1)是否可以仅仅通过某些Pytorch优化器来实现任意的小错误(损失)?由于损失函数是凸的,应该是绝对有可能的,但是,我无法弄清楚,如何使用PyTorch来实现这一点。请注意,上面的3个优化器无法做到这一点--请参阅20000次迭代在日志标度中的丢失进度:
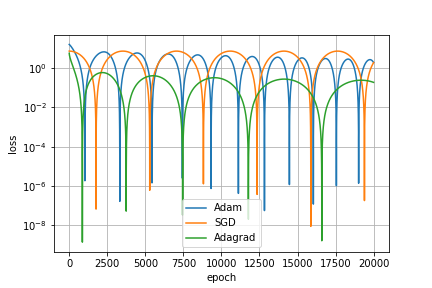
2)我想知道优化器如何能在复杂的例子中很好地工作,即使在这个非常简单的例子中,它们也不能很好地工作。或者(这是第二个问题),我错过了他们在上面的应用中有什么问题吗?
回答 1
Stack Overflow用户
发布于 2020-05-14 17:12:51
你打电话给zero_grad的地方是错的。在每个时代,梯度被添加到前一个,并反向传播。这使得损失随着它的接近而振荡,但先前的梯度又将它从解中抛出。
下面的代码将很容易地执行任务:
import torch
X = torch.randn(1000,1,1)
net = SimpleNet()
optimizer = Adam(params=net.parameters())
for epoch in range(EPOCHS):
optimizer.zero_grad() # zero the gradient buffers
loss = torch.mean((net.forward(X) - X) ** 2)
if loss < 1e-8:
print(epoch, loss)
break
loss.backward()
optimizer.step()( 1)是否可以仅仅通过某些Pytorch优化器来实现任意的小错误(损失)?
是的,以上的精度是在大约1500年代达到的,你可以走到更低的机器(在这种情况下是浮子)精度。
2)我想知道优化器如何能在复杂的例子中很好地工作,即使在这个非常简单的例子中,它们也不能很好地工作。
目前,我们没有比一阶方法更好(至少更广泛)的网络优化方法了。这些方法用于高阶方法,因为计算梯度比Hessians要快得多。而复杂的、非凸的函数可能有大量的极小值来完成我们抛给它的任务,因此不需要全局极小值本身(尽管在某些条件下,它们可以参见本论文)。
https://stackoverflow.com/questions/61801066
复制相似问题

