matlab中的“`fzero`”函数找不到根,继续产生错误
我正在使用MATLAB,我想找到一个方程F(x)-u=0的根。在这里,u=0.2861和
F=normcdf(sqrt(lambda/t)*(t/mu-1))+exp(2*lambda/mu)*normcdf(-sqrt(lambda/t)*(t/mu+1)).lambda和mu的值都是1。
我输入了以下代码
[x,fval] = fzero(@(t) normcdf(sqrt(lambda/t)*(t/mu-1))+exp(2*lambda/mu)*normcdf(-sqrt(lambda/t)*(t/mu+1))-u, 10);希望这能帮我找到根。我可以从数学上证明这个方程有唯一的根。但是,我继续得到以下错误
使用
erfc输入时出错必须是真实的和完整的.normcdf>localnormcdf中的错误(第128行)p(todo) = 0.5 * erfc(-z ./ sqrt(2));normcdf中的错误(第50行)[varargout{1:max(1,nargout)}] = localnormcdf(uflag,x,varargin{:});Test>@(t)normcdf(sqrt(lambda/t)*(t/mu-1))+exp(2*lambda/mu)*normcdf(-sqrt(lambda/t)*(t/mu+1))-u中的错误fzero中的错误(第363行)a = x - dx; fa = FunFcn(a,varargin{:});
然后我用了一种“残忍的武力”的方法。
t = [0:0.001:20];
F = normcdf(sqrt(lambda./t).*(t/mu-1))+exp(2*lambda/mu).*normcdf(-sqrt(lambda./t).*(t/mu+1))-u;
plot(t,F)我可以清楚地看到,F(t)-u在t中的含量在增加,根在0.4左右。我的问题是,为什么fzero在这种情况下不能工作,是否有办法使fzero工作?
回答 1
Stack Overflow用户
发布于 2020-03-26 10:26:56
问题是函数不改变符号,正如文档所说的那样,这是必需的:
x = fzero(fun,x0)试图找到一个x点,其中fun(x) = 0。这个解决方案是fun(x)更改符号的地方--fzero找不到像x^2这样的函数的根。
我分解了您的代码以使其更加清晰(至少对我来说是这样)。
lambda = 1;
mu = 1;
u = 1;
% break up function code
arg1 = @(t) +sqrt(lambda./t).*(t./mu-1);
arg2 = @(t) -sqrt(lambda./t).*(t./mu+1);
fnc = @(t) normcdf(arg1(t))+exp(2*lambda/mu).*normcdf(arg2(t))-u;
% call fzero to find the root
% [x,fval] = fzero(fnc, 10);
% plot
x = 0:0.01:10;
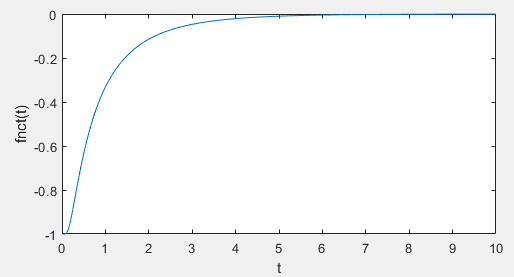
plot(x,fnc(x))函数没有为任何输入t <0定义,因为函数句柄arg中的sqrt。因此,如果将其绘制为值t > 0,则会看到它从未传递过零。
编辑:符号混合在参数中。因为他指出了这一点。绘图和代码更新。这一论点仍然成立。
https://stackoverflow.com/questions/60863393
复制相似问题

