R中截尾积分函数的奇异性
R中截尾积分函数的奇异性
提问于 2020-02-26 11:48:54
从数学上讲,以下是不可能的
library(truncdist)
q = function(x, L, R ) dtrunc(x, "exp", rate=0.1, a=L,b=R)
integrate(q, L=2, R=3, lower =0, upper = 27 )
integrate(q, L=2, R=3, lower =0, upper = 29 )
integrate(q, L=2, R=3, lower =27, upper = 29 )
integrate(q, L=2, R=3, lower =0, upper = 30 )我们发现第一个积分给出了一个正数,第二个积分是通过增加第三个积分区间来求零的,第三个区间积分到零。这是integrate还是truncdist中的一个问题?
我们可以使用以下方法找到更多这样的问题
z=numeric()
for(i in 1:50){
z[i]=integrate(q, L=2, R=3, lower =0, upper = i)$value
}我需要做什么才能找到正确的积分(当从0到i>=3集成时,所有积分都是1)?
回答 2
Stack Overflow用户
回答已采纳
发布于 2020-02-26 12:30:21
来自help("integrate")
和所有的数值积分例程一样,它们在有限点集上计算函数。如果该函数在其几乎所有范围内近似为常数(特别是零),则结果和误差估计可能严重错误。
您找到了一个这样的例子:
curve(q(x, 2, 3), from = -1, to = 30)
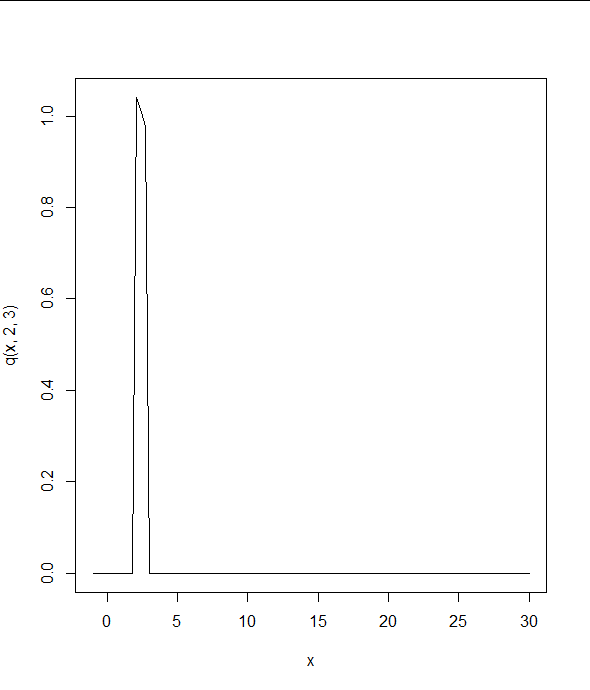
你不应该用数值积分分布密度函数。使用累积分布函数:
diff(ptrunc(c(0, 29), "exp", rate = 0.1, a = 2, b = 3))
#[1] 1Stack Overflow用户
发布于 2021-04-16 14:24:19
我在这篇文章中找到了另一个答案:Integration in R with integrate function
使用hcubature可以数值求解这个问题,这是一个更接近于我原来的问题的答案。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/60413266
复制相关文章
相似问题

