为什么numpy把小数字当作零呢?
为什么numpy把小数字当作零呢?
提问于 2020-02-04 12:52:39
我在做优化任务。考虑两个维度中的“球基准函数”。
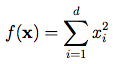
import numpy as np
x = y = 0
X = np.array([x, y])
cost = np.sum(X**2)
print(cost) # zero当x和y为零时,函数的成本为零。但是,请考虑下面的示例:
import numpy as np
X = np.array([-6.5333928195191023e-163, 2.7628829205465545e-163])
Y = X**2 # [0, 0]
cost = np.sum(Y) # zero
print(cost) # zero成本不应该是零,但确实是零。有办法解决这个问题吗?
回答 1
Stack Overflow用户
回答已采纳
发布于 2020-02-04 13:01:58
正常的浮点精度会将您的数字截断为零。如果您真的想使用这么小的值,您可以:
X = np.array([-6.5333928195191023e-163, 2.7628829205465545e-163], dtype=np.longdouble)
Y = X**2 # [0, 0]
cost = np.sum(Y) # zero
print(cost) # zero
>> 5.0318743766791623303e-325页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/60057870
复制相关文章
相似问题

