是否可以用射线追踪器渲染莫比乌斯带?
是否可以用射线追踪器渲染莫比乌斯带?
提问于 2020-01-18 22:36:52
在我的射线追踪器中,所有的表面都是以原点为中心,并以Y轴为取向。通过对射线的变换矩阵,得到位移、旋转和尺寸。
最近,我用笛卡儿方程在光线追踪中绘制了一个圆环:
(x^2 + y^2 + z^2) ^2-2* (r1^2 + r2^2) * (x^2 + y^2 +z^2)+4* r1^2 * y^2 + (r1^2 - r2^2)^2
我用射线方程代替了每一点:
X= Ray.ori.x +T* Ray.dir.x;
用射线分量代替方程中的射线分量,得到四次函数的5个系数,用四次多项式求解算法求出方程的根(T交)。
我想知道是否可以以同样的方式呈现mobius条。我的研究没有提到太多,我发现了一些使用立方方程的射线追踪码,但是复制了这4个系数,我发现了难以理解的形式和人工产物。
你能帮我把它渲染一下吗?另外,还可以建议使用另一种方法来呈现它。
谢谢!
回答 3
Stack Overflow用户
回答已采纳
发布于 2020-02-14 01:55:25
是的,它是可以渲染一个莫比乌斯带的射线追踪。
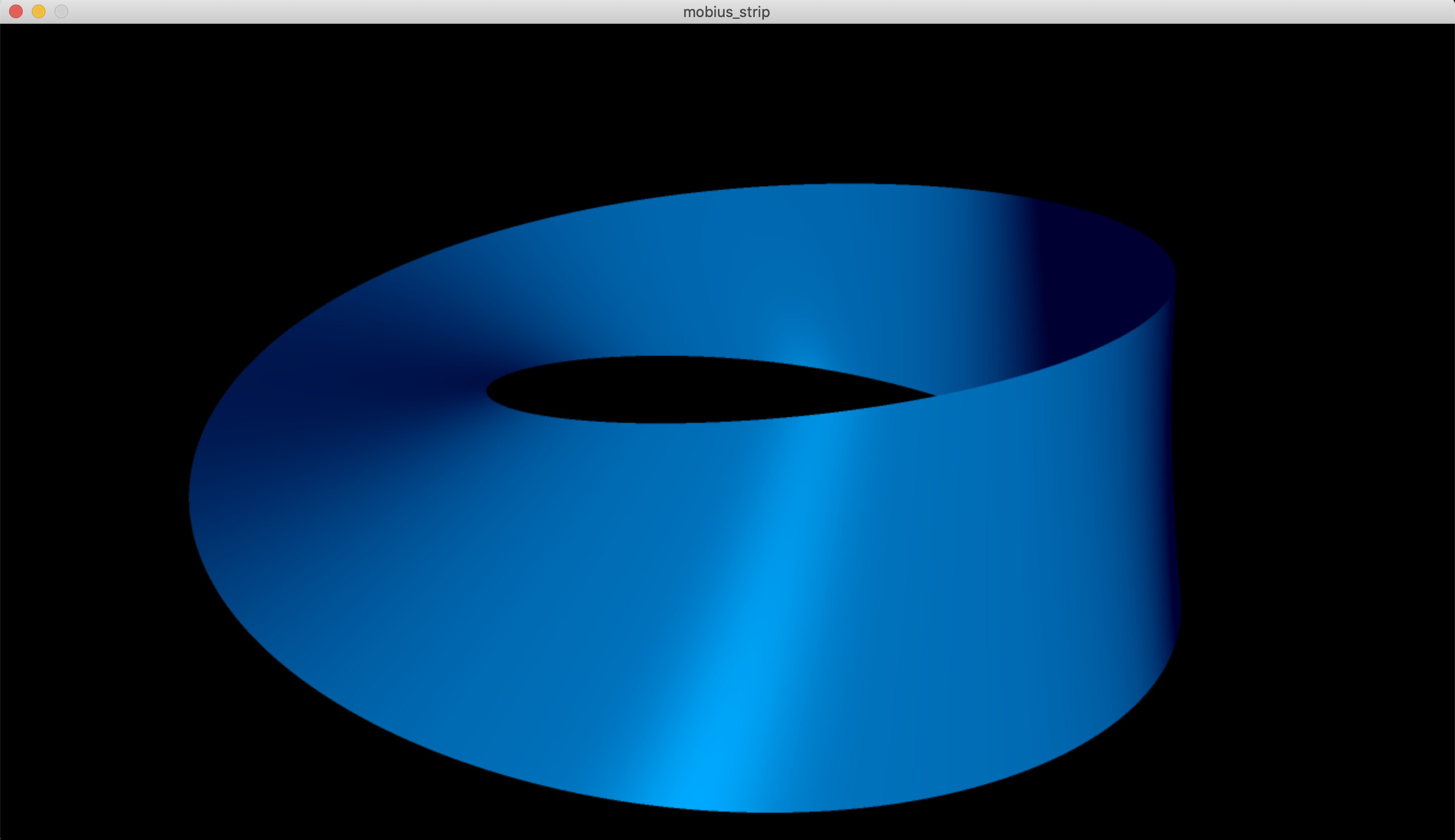
Stack Overflow用户
发布于 2020-01-19 19:37:59
我从:数学世界取了摩比乌斯的(笛卡尔)立方方程,然后用射线方程代替了莫比乌斯的x,y和z。
然而,其结果是:

这是计算mobius系数的代码。
double x = ray.ori.x;
double y = ray.ori.y;
double z = ray.ori.z;
double i = ray.dir.x;
double j = ray.dir.y;
double k = ray.dir.z;
double c[4];
double R = 1.;
int solutions;
c[3] = (i * i) * j - 2. * (i * i) * k + (j * j * j) - 2. * (j * j) * k + j * (k * k);
c[2] = (i * i) * y - 2. * (i * i) * z + 2 * i * j * x - 2. * i * k * R - 4. * i * k * x + 3. * (j * j) * y - 2. * (j * j) * z - 4. * j * k * y + 2. * j * k * z + (k * k) * y;
c[1] = - 2. * i * R * z + 2 * i * x * y - 4. * i * x * z - j * (R * R) + j * (x * x) + 3. * j * (y * y) - 4. * j * y * z + j * (z * z) - 2. * k * R * x - 2 * k * (x * x) - 2. * k * (y * y) + 2. * k * y * z;
c[0] = - (R * R) * y - 2. * R * x * z + (x * x) * y - 2. * (x * x) * z + (y * y * y) - 2. * (y * y) * z + y * (z * z);也许我是在绘制延伸到无限大的整个表面?在这种情况下如何得到莫比乌斯带?
Stack Overflow用户
发布于 2022-08-24 19:54:07
你的最后一篇文章是对的。你确实是在渲染良好的3d形状。
要得到你的莫比乌斯条,你只需要选择正确的部分。
你可能想把你的笛卡尔方程和你在维基百科上找到的参数方程相加在一个3d绘图工具中。
然后你会看到它在哪里;)
(中心是原点,半径为1.5)
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/59805509
复制相关文章
相似问题

