用为地面真相定义的相同颜色着色以进行可视化。
示例:(考虑一下平台= MATLAB)
Ground_Truth_Indices = [ 1, 1, 1, 2, 2, 2, 3, 3, 3];对于GT中的每个唯一索引,我已经定义了一个颜色数组。
Color_Array = [ 0, 255, 0; 255, 0, 0; 0, 0, 255]; %assuming (in this eg.) the max. cluster size is 3接下来,我使用了一个聚类算法(在我的例子中是DBSCAN),它给出了以下索引:
Clustered_Indices = [2, 2, 2, 3, 3, 3, 1, 1, 1];现在,我需要可视化的结果与地面真相。但聚类后得到的指标与地面真实指数不同。
因此,,根据定义的颜色数组,对于地面真相,我将不会得到相同的颜色模式,并在可视化过程中获得簇。有什么解决办法让我可以使两种颜色一致吗?
图中的链接(不是MatLab图)也说明了这一点!为了说明而创建的),其中集群1应该有相同的颜色在地面真相以及获得的集群结果。但是,这里的情况并非如此,因为定义了与颜色数组相关联的索引数。
注:聚类后得到的指标不能预定义,取决于聚类算法和聚类输入。
回答 2
Stack Overflow用户
发布于 2019-11-24 08:43:41
您可以使用Kuhn最大匹配(匈牙利算法)来找到集群标签的最佳1:1对齐。
由于生成的集群可能有不同数量的集群,因此需要一个健壮的实现,可以在非平方矩阵中找到对齐。
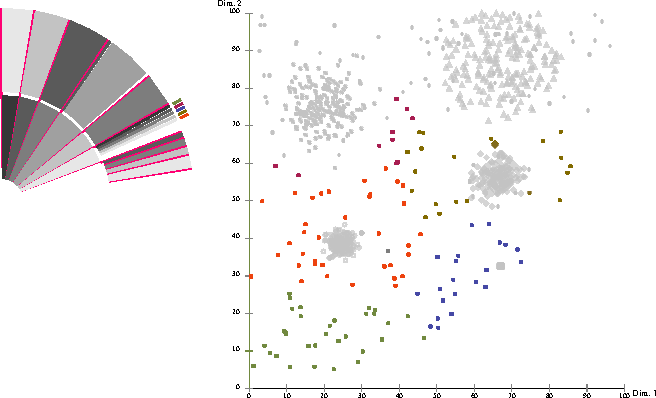
但是,您可能更感兴趣的是想象出集群之间的差异。我在下面的文章中看到了这一点,但我不确定它是否可以用于玩具数据集之外:
聚类评价--计量与视觉支持埃尔克·艾克特,萨沙·戈德霍弗,+2作者亚瑟·齐梅克发表在IEEE28国际…杂志上2012年DOI:10.1109/ICDE.2012.128
(不好意思,不完整的引用,归咎于语义学者,但这是最容易链接的数字从论文,我不能采取一个更好的屏幕截图在这个设备)。
这似乎形象化了k均值和EM聚类之间的差异,其中灰色点是它们在聚类上达成一致的地方。这种方法似乎适用于对点,就像评价措施一样。
Stack Overflow用户
发布于 2019-11-30 06:34:38
由于本文的答案是:如何将集群标签与Matlab中的“基本真理”标签相匹配,我有以下解决方案代码来解决我的问题:
N = length(Ground_Truth_Indices);
cluster_names = unique(Clustered_Indices);
accuracy = 0;
maxInd = 1;
perm = perms(unique(Ground_Truth_Indices));
[perm_nrows perm_ncols] = size(perm);
true_labels = Ground_Truth_Indices;
for i=1:perm_nrows
flipped_labels = zeros(1,N);
for cl = 1 : perm_ncol
flipped_labels(Clustered_Indices==cluster_names(cl)) = perm(i,cl);
end
testAcc = sum(flipped_labels == Ground_Truth_Indices')/N;
if testAcc > accuracy
accuracy = testAcc;
maxInd = i;
true_labels = flipped_labels;
end
end其中,'true_labels‘包含变量'Clustered_Indices’的重新排列的标签,该标签与变量‘接地_真理_指数’相一致。
正如在最初的文章中所解释的那样,这段代码使用了基于置换的匹配(对于我在这篇文章中给出的示例来说,它非常有效。我还测试了其他变体)。但是,当集群的大小变大时,该代码不能正常工作。你对这段代码怎么看?有更好的方法来写吗?还是优化它?
https://stackoverflow.com/questions/59014629
复制相似问题

