用astropy.modeling拟合负振幅高斯问题
用astropy.modeling拟合负振幅高斯问题
提问于 2020-01-27 17:55:24
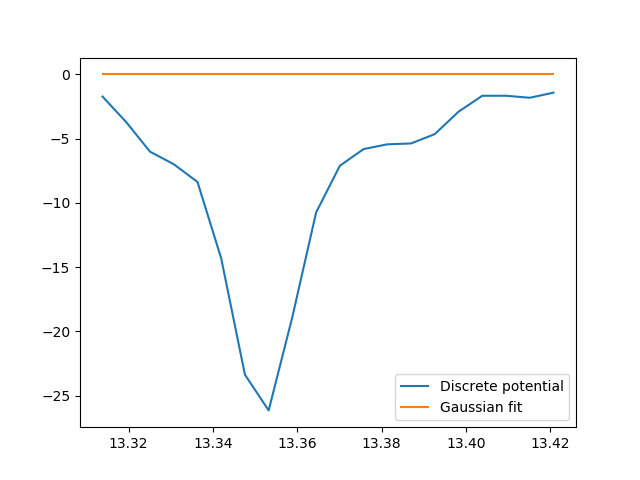
我试图用astropy.modeling软件包来拟合高斯到离散势。虽然我给高斯分配了一个负振幅,但是它返回一个零的高斯,也就是说,到处都是零振幅:
plot(c[0], pot_x, label='Discrete potential')
plot(c[0], g(c[0]), label='Gaussian fit')
legend()
我有以下代码行来执行安装:
g_init = models.Gaussian1D(amplitude=-1., mean=0, stddev=1.)
fit_g = fitting.LevMarLSQFitter()
g = fit_g(g_init, c[0], pot_x)哪里
c[0] = array([13.31381488, 13.31944489, 13.32507491, 13.33070493, 13.33633494,
13.34196496, 13.34759498, 13.35322499, 13.35885501, 13.36448503,
13.37011504, 13.37574506, 13.38137507, 13.38700509, 13.39263511,
13.39826512, 13.40389514, 13.40952516, 13.41515517, 13.42078519])
pot_x = array([ -1.72620157, -3.71811187, -6.01282809, -6.98874144,
-8.36645166, -14.31787771, -23.3688849 , -26.14679496,
-18.85970983, -10.73888697, -7.10763373, -5.81176637,
-5.44146953, -5.37165105, -4.6454408 , -2.90307138,
-1.66250349, -1.66096343, -1.8188269 , -1.41980552])有人有想法吗?问题可能是什么?
解决了:我只需要分配一个在域范围内的平均值,比如13.35。
回答 1
Stack Overflow用户
发布于 2020-01-27 18:56:53
因为我对Astropy不熟悉,所以我用了scipy。下面的代码提供了以下输出:
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import curve_fit
x = np.asarray([13.31381488, 13.31944489, 13.32507491, 13.33070493, 13.33633494,
13.34196496, 13.34759498, 13.35322499, 13.35885501, 13.36448503,
13.37011504, 13.37574506, 13.38137507, 13.38700509, 13.39263511,
13.39826512, 13.40389514, 13.40952516, 13.41515517, 13.42078519])
y = -np.asarray([ -1.72620157, -3.71811187, -6.01282809, -6.98874144,
-8.36645166, -14.31787771, -23.3688849 , -26.14679496,
-18.85970983, -10.73888697, -7.10763373, -5.81176637,
-5.44146953, -5.37165105, -4.6454408 , -2.90307138,
-1.66250349, -1.66096343, -1.8188269 , -1.41980552])
mean = sum(x * y) / sum(y)
sigma = np.sqrt(sum(y * (x - mean)**2) / sum(y))
def Gauss(x, a, x0, sigma):
return a * np.exp(-(x - x0)**2 / (2 * sigma**2))
popt,pcov = curve_fit(Gauss, x, y, p0=[max(y), mean, sigma])
plt.plot(x, y, 'b+:', label='data')
plt.plot(x, Gauss(x, *popt), 'r-', label='fit')
plt.legend()
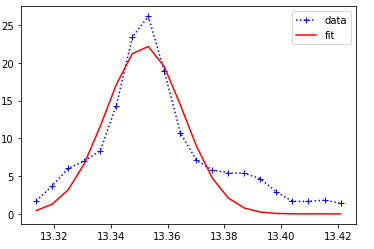
简单地说,我重用了这个answer。我不完全确定平均值和西格玛的定义,因为我不习惯在2D数据集上拟合高斯。但是,这并不重要,因为它只是用来定义一个用于启动curve_fit算法的近似。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/59936456
复制相关文章
相似问题

