如何使用norm.ppf()?
我不知道如何正确地使用这个功能,有人能解释一下吗?
假设我有:
- 平均数为172.7815
- 标准差4.1532
- N= 50 (50个样本)
当我被要求使用norm.ppf()计算(95%)错误裕度时,代码是否如下所示?
norm.ppf(0.95, loc=172.78, scale=4.15)还是看起来像这样?
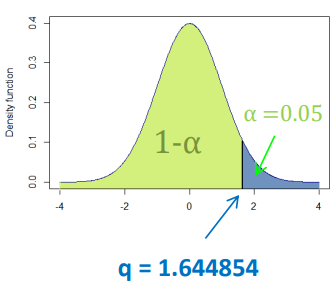
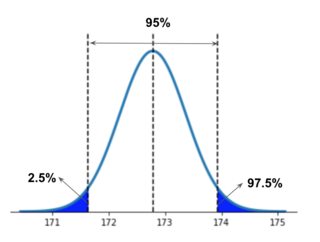
norm.ppf(0.95, loc=0, scale=1)因为我知道它在计算置信区间右边的曲线面积(95%,97.5%的etc...see图像),但是当我有一个平均值和一个标准差时,我真的很困惑如何使用这个函数。
回答 5
Stack Overflow用户
发布于 2020-05-02 08:37:08
方法norm.ppf()获取一个百分比,并返回该百分比值的标准差乘数。
它相当于密度图上的“单尾检验”。
来自scipy.stats.norm:
ppf(q,loc=0,scale=1)百分比函数( cdf百分位数的逆).
标准正态分布
守则:
norm.ppf(0.95, loc=0, scale=1)返回标准正态分布上的单尾检验的95%显着性区间(即均值为0,标准差为1的正态分布的特例)。
我们的示例
为了计算我们95%的显着性间隔所在的OP提供的示例的值(对于一个尾检验),我们将使用:
norm.ppf(0.95, loc=172.7815, scale=4.1532)这将返回一个值(该值作为multiplier')标记的的标准差,如果我们的数据是正态分布的话,95%的数据点将被包含其中。)
为了得到精确的数,我们取norm.ppf()输出,并将其乘以对所述分布的标准差。
A双尾测试
如果我们需要计算一个“双尾检验”(即我们所关心的数值大于或小于我们的平均值),那么我们需要除以重要性(即我们的alpha值),因为我们仍然在使用一条尾巴的计算方法。分裂成两半,象征着对两个尾巴的意义水平。95%的显着性水平有5%的阿尔法;将5%的α分成两尾,结果为2.5%。取2.5%从100%返回97.5%作为显着性水平的输入。
因此,如果我们关注均值两边的值,我们的代码将输入.975来表示跨越两个尾的95%的显着性级别:
norm.ppf(0.975, loc=172.7815, scale=4.1532)误差裕度
误差裕度是用样本统计量估计总体参数时所使用的显着性水平。我们希望使用对的双尾输入来生成95%的置信区间,因为我们关注的值大于或小于平均值:
ppf = norm.ppf(0.975, loc=172.7815, scale=4.1532)接下来,我们取ppf并乘以标准差返回区间值:
interval_value = std * ppf最后,通过从平均值中添加和减去区间值来标记置信区间:
lower_95 = mean - interval_value
upper_95 = mean + interval_value用垂直线绘制:
_ = plt.axvline(lower_95, color='r', linestyle=':')
_ = plt.axvline(upper_95, color='r', linestyle=':')Stack Overflow用户
发布于 2021-08-25 18:01:17
詹姆斯关于norm.ppf返回一个“标准差乘数”的说法是错误的。这感觉很贴切,因为当你搜索norm.ppf时,他的帖子是谷歌排名第一。
'norm.ppf‘是’Nor.cdf‘的反义词。在本例中,它只返回95%百分位数的值。不涉及“标准差乘数”。
这里有一个更好的答案:如何计算python中正态分布累积分布函数的逆?
Stack Overflow用户
发布于 2021-03-14 07:51:06
您可以直接用norm.ppf计算置信区间,而不需要计算误差裕度。
upper_of_interval = norm.ppf(0.975, loc=172.7815, scale=4.1532/np.sqrt(50))
lower_of_interval = norm.ppf(0.025, loc=172.7815, scale=4.1532/np.sqrt(50))4.1532是样本标准差,而不是样本均值样本分布的标准差。因此,scale在norm.ppf中将被指定为scale = 4.1532 / np.sqrt(50),它是抽样分布标准差的估计量。
(抽样分布的标准差等于population standard deviation / np.sqrt(sample size)。在这里,我们不知道总体标准差和样本规模大于30,所以sample standard deviation / np.sqrt(sample size)可以作为一个很好的估计器)。
误差裕度可以用(upper_of_interval - lower_of_interval) / 2计算。
https://stackoverflow.com/questions/60699836
复制相似问题

