N维数据经验分布估计的累积概率
问题所在
我有一个具有4个数字特性和1000个数据点的数据集。值的分布是未知的(numpy randint生成统一的ints,但这只是为了说明目的)。给定新的数据点(4个数字),我想知道这个特定数据点的累积概率(单个数字)是多少。
import numpy as np
data = np.random.randint(1, 100, size=(1000, 4))
array([[28, 52, 91, 66],
[78, 94, 95, 12],
[60, 63, 43, 37],
...,
[81, 68, 45, 46],
[14, 38, 91, 46],
[37, 51, 68, 97]])
new_data = np.random.randint(1, 100, size=(1, 4))
array([[75, 24, 39, 94]])我试过:
Scipy
可以估计pdf,不知道如何估计累积概率。可能的方法是蒙特卡洛模拟或集成(scipy.integrate.nquad),这对我的例子Integrate 2D kernel density estimate来说太慢了。
import scipy.stats
kde = scipy.stats.gaussian_kde(data.T)
kde.pdf(new_data)Scikit-学习
与上述相同,不知道如何估计累积概率。
from sklearn.neighbors import KernelDensity
model = KernelDensity()
model.fit(data)
np.exp(model.score_samples(new_data))状态模型
不能存档任何东西,因为这只接受一维数据。
from statsmodels.distributions.empirical_distribution import ECDF
ecdf = ECDF(data[:, 0])
ecdf(new_data[0][0])的问题是,是否有一种快速有效的方法来估计具有所提供的枕木或滑雪板模型的四维数据点的累积概率?
我是朝着正确的方向前进,还是有完全不同的方法来解决这个问题?也许变分的自动编码器是一条路?有简单的方法来解决这个问题吗?
回答 2
Stack Overflow用户
发布于 2020-04-22 15:44:23
在一个点上的多变量ecdf只会用值小于点的值计算观测值的分数。
如下所示
np.random.seed(0)
data = np.random.randint(1, 100, size=(1000, 4))
new_data = np.random.randint(1, 100, size=(2, 4))
def ecdf_mv(new_data, data):
new_data = np.atleast_2d(new_data)
ecdf = []
for row in new_data:
ecdf.append((data <= row).all(1).mean())
return np.asarray(ecdf)
ecdf_mv(new_data, data)
array([0.039, 0.002])一些支票:
ecdf_mv(np.ones(4) * 100 / 2, data), 0.5**4
(array([0.067]), 0.0625)
marginal = 100 * np.ones((4, 4)) - 50 * np.eye(4)
ecdf_mv(marginal, data)
array([0.521, 0.515, 0.502, 0.54 ])在单变量情况下,我们可以对数据进行排序,得到一个快速算法来计算原始点的ecdf。
我不知道是否有比蛮力比较计算更有效的数据结构或算法,如果必须在多个点上对ecdf进行评估。
Stack Overflow用户
发布于 2021-12-11 17:27:20
通过尝试和错误,我发现了以下几点:
一个纯粹的numpy解决方案(基于Josef的):
import numpy as np
def ecdf_mv(new_data, data):
rows = np.expand_dims(new_data, axis=1)
ecdf = (data < rows).all(axis=2).mean(axis=1)
return np.asarray(ecdf)这将返回一个点数组的经验累积分布函数。
如果希望使用多变量KDE上的CDF,则可以使用以下代码(但这要慢得多):
from statsmodels.nonparametric.kernel_density import KDEMultivariate
def cdf_kde_mv(new_data, data, data_type):
data_kde = KDEMultivariate(data, var_type=data_type)
return data_kde.cdf(new_data)就性能而言,纯numpy可能更快,但内存更密集,而Josef使用for-循环的方法在某些情况下更快。
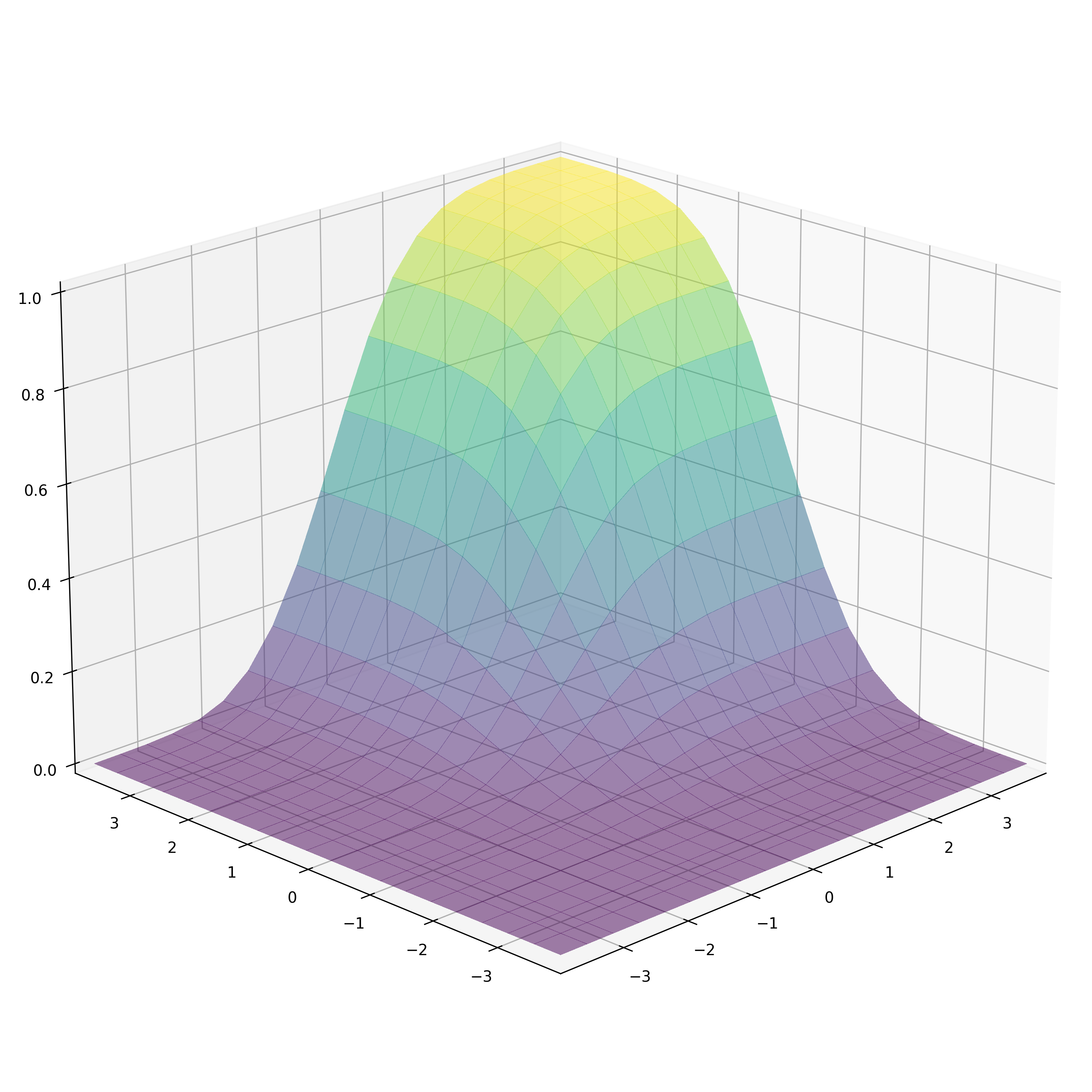
对于“烟雾”的感觉,它不是取决于“相对于多元KDE”的"ECDF“,而是更多地依赖于你的样本大小和回收箱的数量。在下面的示例中,即使不使用KDE,可视化看起来也是“平滑的”,这是因为样本的大小足以容纳那么多的回收箱。被解释为平滑的插值是matplotlib plot_surface。如果您还需要平滑的结果分析,而不仅仅是对图,考虑使用KDE方法。
将其应用于一些可视化操作:
import numpy as np
import matplotlib.pyplot as plt
sample_size = 10_000
bins_count= 20
sample = np.random.multivariate_normal([0, 0], [[1, 0.0], [0.0, 1]] , sample_size)
bins_edges = np.linspace(-4, 4, bins_count + 1)
bins_centers = (bins_edges[:-1] + bins_edges[1:]) / 2
X, Y = np.meshgrid(bins_centers, bins_centers)
x, y = X.ravel(), Y.ravel()
evaluation_points = np.stack([x, y], axis=1)
cummulative_probability = cdf_kde_mv(evaluation_points, sample, "cc")
# Alternatively:
cummulative_probability = ecdf_mv(evaluation_points, sample)
cummulative_probability = cummulative_probability.reshape(bins_count, bins_count)
# Plotting
fig = plt.figure(figsize=(10, 10), constrained_layout=True)
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=20., azim=-135)
ax.plot_surface(X, Y, cummulative_probability, rcount=bins_count, ccount=bins_count,
antialiased=False, vmin=0, vmax=cummulative_probability.max(),
alpha=0.5, cmap='viridis')
ax.margins(0)
ax.set_zlim(0, 1)
plt.show()
https://stackoverflow.com/questions/61363896
复制相似问题

