定义二维网格的算法
假设网格由一组网格参数定义:它的起源(x0,y0),天使
在一侧和x轴之间,以及增量
和
- 请看下图。
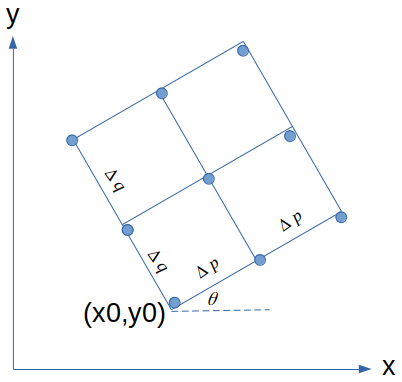
网格上有一些已知坐标的零散点,但它们并不完全落在网格交叉口上。是否有一种算法可以找到一组网格参数来定义网格,以便这些点最适合网格交叉口?
假设已知坐标是:(2,5.464 ),(3.732,6.464),(5.464,7.464) (3,3.732),(4.732,4.732),(6.464,5.732) (4,2 ),(5.732,3 ),(7.464,4)。我期望算法能找到原点(4,2),角度30度,并同时增加2。
回答 2
Stack Overflow用户
发布于 2020-12-18 18:33:53
你可以通过找到一个矩阵将点从(0,0),(0,1),……(2,2)转换成给定的点来解决这个问题。
虽然网格只有5个自由度(原点+角度+尺度的位置),但是用2x3矩阵A来定义变换比较容易,因为在这种情况下,这个问题是线性的。
设一个索引点(x0,y0)被转化为网格上的点(x0',y0'),例如(0,0) -> (2,5.464),并且a_ij是矩阵A的系数。然后,这对点得到两个方程:
a_00 * x0 + a_01 * y0 + a_02 = x0'
a_10 * x0 + a_11 * y0 + a_12 = y0'未知数是a_ij,所以这些方程可以用形式写成。
a_00 * x0 + a_01 * y0 + a_02 + a_10 * 0 + a_11 * 0 + a_12 * 0 = x0'
a_00 * 0 + a_01 * 0 + a_02 * 0 + a_10 * x0 + a_11 * y0 + a_12 = y0'或以矩阵形式
K0 * (a_00, a_01, a_02, a_10, a_11, a_12)^T = (x0', y0')^T哪里
K0 = (
x0, y0, 1, 0, 0, 0
0, 0, 0, x0, y0, 1
)对于每一对点,这些方程可以合并成一个方程。
K * (a_00, a_01, a_02, a_10, a_11, a_12)^T = (x0', y0', x1', y1', ..., xn', yn')^T或者K * a = b
K = (
x0, y0, 1, 0, 0, 0
0, 0, 0, x0, y0, 1
x1, y1, 1, 0, 0, 0
0, 0, 0, x1, y1, 1
...
xn, yn, 1, 0, 0, 0
0, 0, 0, xn, yn, 1
)(xi, yi), (xi', yi')是对应点对
这可以作为一个非齐次线性方程组来求解.在这种情况下,解决方案将最小化从每个点到最近的网格交点的距离平方之和。这种变换也可以考虑最大的整体可能性,假设点从正态分布噪声的网格交叉口转移。
a = (K^T * K)^-1 * K^T * b如果有一个线性代数库,这个算法可以很容易地实现。下面是Python中的一个示例:
import numpy as np
n_points = 9
aligned_points = [(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)]
grid_points = [(2, 5.464), (3.732, 6.464), (5.464, 7.464), (3, 3.732), (4.732, 4.732), (6.464, 5.732), (4, 2), (5.732, 3), (7.464, 4)]
K = np.zeros((n_points * 2, 6))
b = np.zeros(n_points * 2)
for i in range(n_points):
K[i * 2, 0] = aligned_points[i, 0]
K[i * 2, 1] = aligned_points[i, 1]
K[i * 2, 2] = 1
K[i * 2 + 1, 3] = aligned_points[i, 0]
K[i * 2 + 1, 4] = aligned_points[i, 1]
K[i * 2 + 1, 5] = 1
b[i * 2] = grid_points[i, 0]
b[i * 2 + 1] = grid_points[i, 1]
# operator '@' is matrix multiplication
a = np.linalg.inv(np.transpose(K) @ K) @ np.transpose(K) @ b
A = a.reshape(2, 3)
print(A)[[ 1. 1.732 2. ]
[-1.732 1. 5.464]]然后可以从这个矩阵中提取参数:
theta = math.degrees(math.atan2(A[1, 0], A[0, 0]))
scale_x = math.sqrt(A[1, 0] ** 2 + A[0, 0] ** 2)
scale_y = math.sqrt(A[1, 1] ** 2 + A[0, 1] ** 2)
origin_x = A[0, 2]
origin_y = A[1, 2]theta = -59.99927221917264
scale_x = 1.99995599951599
scale_y = 1.9999559995159895
origin_x = 1.9999999999999993
origin_y = 5.464然而,还有一个小问题:矩阵A对应于仿射变换。这意味着网格轴不能保证垂直。如果这是一个问题,那么矩阵的前两列可以用这样的方式修改,即变换保持角度。
Stack Overflow用户
发布于 2020-12-20 11:57:03
更新:I修复了错误并解决了符号歧义,所以现在这个算法产生了预期的结果。然而,应该对其进行测试,以确定是否正确地处理了所有案件。
这是解决这个问题的另一个尝试。其思想是将变换分解为非均匀尺度矩阵和旋转矩阵A = R * S,然后求解这些矩阵的系数sx, sy, r1, r2,并给出r1^2 + r2^2 = 1的约束条件。最小化问题在这里描述:How to find a transformation (non-uniform scaling and similarity) that maps one set of points to another?
def shift_points(points):
n_points = len(points)
shift = tuple(sum(coords) / n_points for coords in zip(*points))
shifted_points = [(point[0] - shift[0], point[1] - shift[1]) for point in points]
return shifted_points, shift
n_points = 9
aligned_points = [(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)]
grid_points = [(2, 5.464), (3.732, 6.464), (5.464, 7.464), (3, 3.732), (4.732, 4.732), (6.464, 5.732), (4, 2), (5.732, 3), (7.464, 4)]
aligned_points, aligned_shift = shift_points(aligned_points)
grid_points, grid_shift = shift_points(grid_points)
c1, c2 = 0, 0
b11, b12, b21, b22 = 0, 0, 0, 0
for i in range(n_points):
c1 += aligned_points[i][0] ** 2
c2 += aligned_points[i][0] ** 2
b11 -= 2 * aligned_points[i][0] * grid_points[i][0]
b12 -= 2 * aligned_points[i][1] * grid_points[i][0]
b21 -= 2 * aligned_points[i][0] * grid_points[i][1]
b22 -= 2 * aligned_points[i][1] * grid_points[i][1]
k = (b11 ** 2 * c2 + b22 ** 2 * c1 - b21 ** 2 * c2 - b12 ** 2 * c1) / \
(b21 * b11 * c2 - b12 * b22 * c1)
# r1_sqr and r2_sqr might need to be swapped
r1_sqr = 2 / (k ** 2 + 4 + k * math.sqrt(k ** 2 + 4))
r2_sqr = 2 / (k ** 2 + 4 - k * math.sqrt(k ** 2 + 4))
for sign1, sign2 in [(1, 1), (-1, 1), (1, -1), (-1, -1)]:
r1 = sign1 * math.sqrt(r1_sqr)
r2 = sign2 * math.sqrt(r2_sqr)
scale_x = -b11 / (2 * c1) * r1 - b21 / (2 * c1) * r2
scale_y = b12 / (2 * c2) * r2 - b22 / (2 * c2) * r1
if scale_x >= 0 and scale_y >= 0:
break
theta = math.degrees(math.atan2(r2, r1))在选择r1_sqr和r2_sqr时可能存在模糊性。起源点可以从aligned_shift和grid_shift中估计,但是我还没有实现它。
theta = -59.99927221917264
scale_x = 1.9999559995159895
scale_y = 1.9999559995159895https://stackoverflow.com/questions/65296743
复制相似问题

