实值阵的rfft幅值
实值阵的rfft幅值
提问于 2021-02-15 14:54:38
我正在计算长度为3000 (以100赫兹采样)的信号的RFFT,其中只有实际值的条目:
from scipy.fft import rfft
coeffs = rfft(values)
coeffs = np.abs(coeffs)使用rfft,我只得到一半的系数,即对称系数被分割(由于实际值输入)。
用coeffs = (2 / len(values)) * coeffs缩放值以得到振幅是正确的吗?
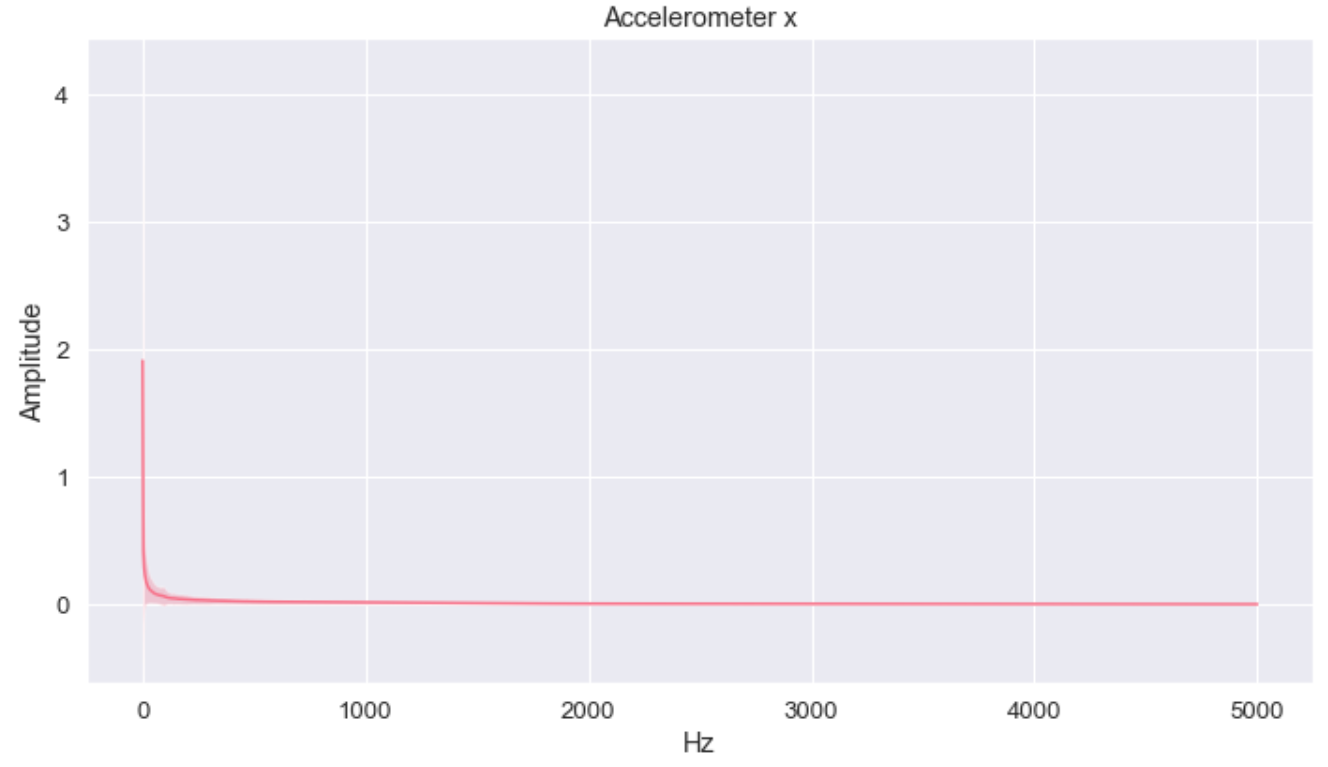
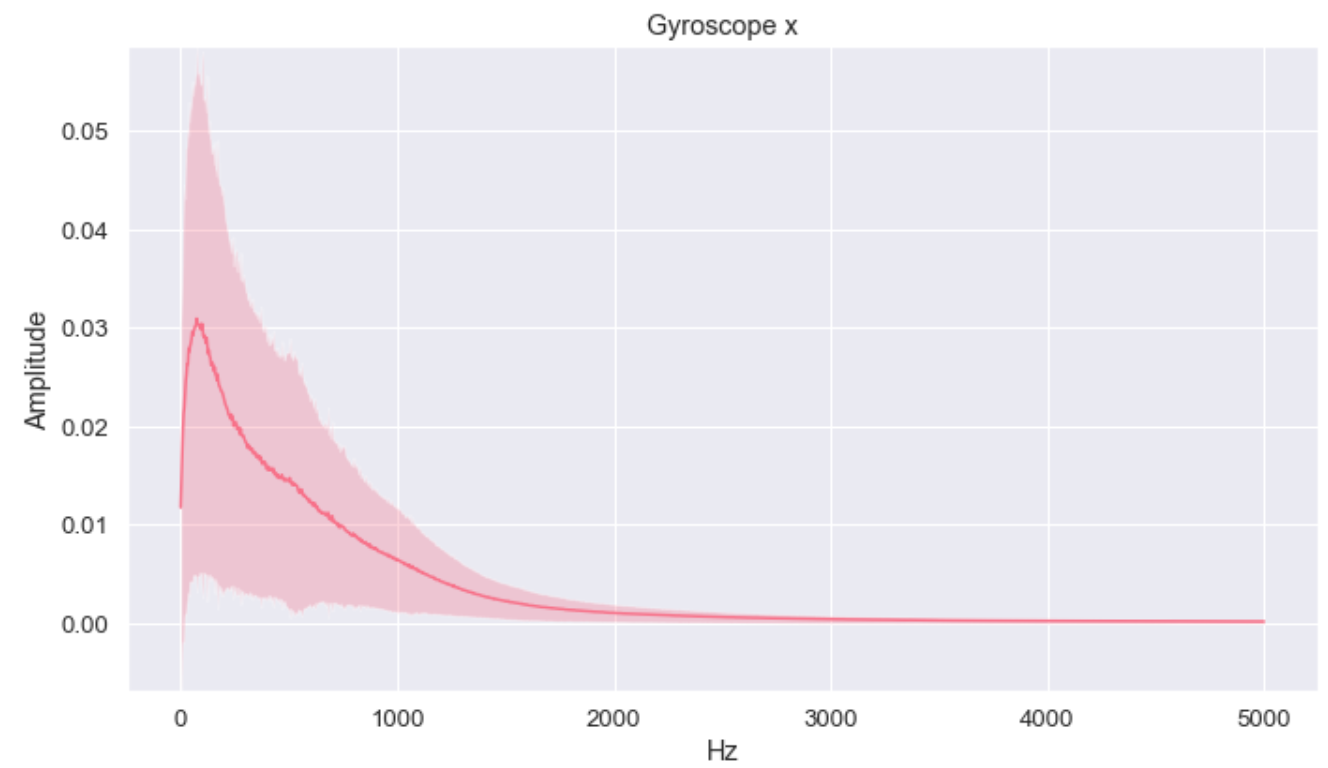
编辑:在下面我已经附上了加速度计和陀螺仪的振幅和频率(bins)的图表(阴影区域是标准偏差)。对于加速度计,第一个FFT仓中的能量远高于其他回收箱中的能量(> 2在第一个垃圾箱中,而在其他垃圾箱中< 0.4左右)。对于陀螺仪来说,它是不同的,能量分布更多。
这是否意味着,对于加速度计,FFT看起来不错,但对于陀螺仪来说,更糟吗?此外,在100赫兹(即仅取回收箱< 100赫兹)或在保持95%的能量之前,将前几个桶切成FFT是否合理?
回答 1
Stack Overflow用户
回答已采纳
发布于 2021-02-16 02:25:21
我在this post中提供的近似关系适用于你是否扔掉一半的系数。
所以,如果那篇文章中指出的条件适用于你的情况,那么你就可以得到一个主要的正弦分量的振幅的估计。
approx_sinusoidal_amplitude = (2 / len(values)) * np.abs(coeffs[k])对于一些指数,k对应于正弦分量的频率(根据我在另一篇文章中指出的限制,这个频率必须在或接近于100/3000 ~ 0.033Hz的倍数。)对于占主导地位的正弦分量,该指数通常对应于频谱中的局部峰值。然而,请注意,如果您的信号是各种频率分量的混合体,那么各个分量可能会以这样一种方式影响频谱,使峰值不明显地出现。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/66210249
复制相关文章
相似问题

