在数组中使用堆栈查找下一个大元素的真正直觉是什么?
在我的面试中,我被问到一个问题,那就是返回ans数组,在其中,ans[i] = next greater element of A[i]和if元素没有下一个更大的-1。
Example:
A = [1, 2, 1, 3, 4]
ans = [2, 3, 3, 4, -1] 我无法给出优化的方法,但我在互联网上搜索,发现我们会用堆栈完成,但我在任何地方都能找到解决问题的方法
如果有人能帮我,那将是一个很大的帮助!:)
回答 2
Stack Overflow用户
发布于 2021-08-31 14:45:46
您可以将输入想象为在垂直条形图中表示条形图。例如:
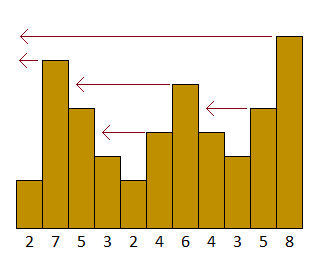
箭头表示较高的杆对其左侧有某种“影响”。你可以想象有人站在酒吧的顶端,朝左边看。或者你可以想到水在这些栅栏之间充满,当它达到当前坝的高度时,你就知道它们的影响范围。当遇到至少有自己高度的条形图时,或者遇到图表的左侧时,它们的影响就停止了。
更高的酒吧通常有更长的影响力,这是有道理的。
现在,当我们从左到右迭代条形图时,我们可以看到如何使用它来生成输出。7对2有影响,因此7被添加到索引0(值2的索引)的输出中。
利率的下一个值是4,它对前两个值有影响,因此在它们的指数(即指数3和4)上,我们应该输出4。
利率的下一个值是6,它对更多的价值有影响,其中只有指数2的5是“新的”。因此,在指数2,我们应该输出6。
我们注意到,对于索引1的输出(包括值7),我们需要继续处理直到达到值8。一些输出可以在同时确定,而7应该“等待”下一个更大的值被找到。
这将给您一种使用堆栈的感觉。对索引4、3、2、1的赋值按反向顺序进行,就像从堆栈中弹出这些索引时得到的一样。在索引1被弹出之前,一些索引将被推送到堆栈中并再次弹出,但最后7也可以弹出,从而结束其更长的等待时间。
此弹出还确保只为输出索引分配一次值。
我意识到你不需要看到算法本身,因为你已经知道了。希望这有助于澄清它背后的直觉是什么。
Stack Overflow用户
发布于 2021-08-31 15:15:55
在A的一个增加部分中,下一个更大的元素就是下一个元素。当有一个下降,你必须等待直到你达到一个更大的价值。
例如。
1, 2, 1, 3, 4可以看作是两个增加的部分。
1, 2||1, 3, 4给下一个更大的元素
2, -||3, 4, -当您到达2 (在原始数组中)时,您必须等到到达3 (在原始数组中)并得出结论
2, 3, 3, 4, -当您到达4 (在原始数组中)时,您必须等待.因为没有更大的元素。
现在,对堆栈的需求源于这样一个事实:如果您从左到右前进,可能会有几个等待元素。由于这些元素构成一个递减部分,它们将首先被“服务”最小,这与LIFO的顺序相对应。
https://stackoverflow.com/questions/68999961
复制相似问题

