如何在随机数据流中调整值的分布?
如何在随机数据流中调整值的分布?
提问于 2010-03-10 20:20:38
给定一个随机0和1的无限流,它来自有偏置(例如,1是比0更常见的已知因素),但如果不是理想的随机数产生器,我想把它转换成(较短的)无限流,它同样是理想的,也是无偏的。
查找熵的定义可以找到这个图表,它显示了理论上我应该从每一位输入中获得多少位输出。
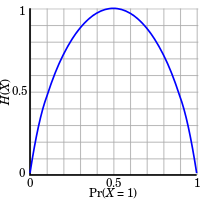
问题是:是否有任何实际的方法来实际实现一个几乎是理想效率的转换器?
回答 3
Stack Overflow用户
发布于 2010-03-10 20:27:31
由于冯·诺依曼()把一枚不公平的硬币变成了一枚公平的硬币,有一个众所周知的装置。我们可以用这个装置来解决我们的问题。
重复地从你的偏置源中画出两个位,直到你得到一个不同位元的对。现在返回第一位,丢弃第二位。这产生了一个不偏不倚的来源。这是因为不管源是什么,01的概率和10的概率是一样的。因此,0条件在01或10上的概率是1/2,1条件在01或10上的概率是1/2。
Stack Overflow用户
发布于 2010-03-10 20:43:03
请参阅
- 萃取器
- 转换
- http://en.wikipedia.org/wiki/Decorrelation
Stack Overflow用户
发布于 2010-05-26 18:09:49
霍夫曼对输入进行编码。
如果输入具有已知的偏差,则可以计算每个n位段的校验和的概率分布。构造一个霍夫曼码,然后对序列进行编码。
我不确定,但一个潜在的问题是,这可能会在序列位之间引入某种相关性。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/2420283
复制相关文章
相似问题

