如何加快最长公共子串长度的计算?
我有两个非常大的字符串,我正在试图找出它们的最长公共子串。
一种方法是使用后缀树(虽然这是一个复杂的实现,但应该具有很好的复杂性),另一种方法是动态编程方法(这两种方法都在上面链接的维基百科页面中提到)。
使用动态规划
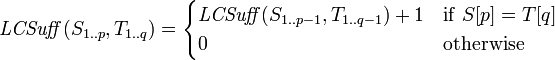
问题是动态规划方法有很长的运行时间(复杂性为O(n*m),其中n和m是两个字符串的长度)。
我想知道的(在跳到实现后缀树之前):如果我只想知道公共子字符串的长度(而不是公共子字符串本身),那么是否有可能加快算法的速度?
回答 4
Stack Overflow用户
发布于 2010-04-25 21:24:17
在实践中它会更快吗?是。对于大-哦,会更快吗?不是的。动态规划解总是O(n*m)。
使用后缀树可能会遇到的问题是,用后缀树的线性时间扫描来换取空间上的巨大损失。后缀树通常比算法的动态编程版本所需实现的表大得多。取决于字符串的长度,动态编程完全可能会更快。
祝你好运:)
Stack Overflow用户
发布于 2010-04-25 21:29:27
这将使它运行得更快,尽管它仍然是O(nm)。
一个优化是在空间(这可能为您节省一点分配时间)注意到LCSuff只取决于上一行--因此,如果您只关心长度,可以将O(nm)空间优化到O(min(n,m))。
这样做的目的是只保留两行--正在处理的当前行和刚刚处理的前一行,并丢弃其余的行。
Stack Overflow用户
发布于 2015-11-16 05:21:28
这里有一个简单的算法,可以在O(m+n) *log(m+n))中完成,与后缀树算法(O(m+n)运行时)相比,实现起来容易得多。
让它以最小公共长度(minL) = 0和最大公共长度(maxL) = min(m+n)+1开始。
1. if (minL == maxL - 1), the algorithm finished with common len = minL.
2. let L = (minL + maxL)/2
3. hash every substring of length L in S, with key = hash, val = startIndex.
4. hash every substring of length L in T, with key = hash, val = startIndex. check if any hash collision in to hashes. if yes. check whether whether they are really common substring.
5. if there're really common substring of length L, set minL = L, otherwise set maxL = L. goto 1.剩下的问题是如何在时间O(n)中散列长度为L的所有子字符串。您可以使用如下多项式公式:
Hash(string s, offset i, length L) = s[i] * p^(L-1) + s[i+1] * p^(L-2) + ... + s[i+L-2] * p + s[i+L-1]; choose any constant prime number p.
then Hash(s, i+1, L) = Hash(s, i, L) * p - s[i] * p^L + s[i+L];https://stackoverflow.com/questions/2710010
复制相似问题

