问包含原始详细多边形的简化(或光滑)多边形

EN

编辑

截至2013年，下面的大多数链接都不再运行了。然而，我找到了引用的论文，包括算法，仍然可以在这个(非常慢)的服务器上使用。。

这里 --您可以找到一个处理问题的项目。虽然它主要用于按点“填充”的区域，但您可以将其设置为使用“外围”类型定义。

它使用k近邻方法来计算区域.

示例：

​

​

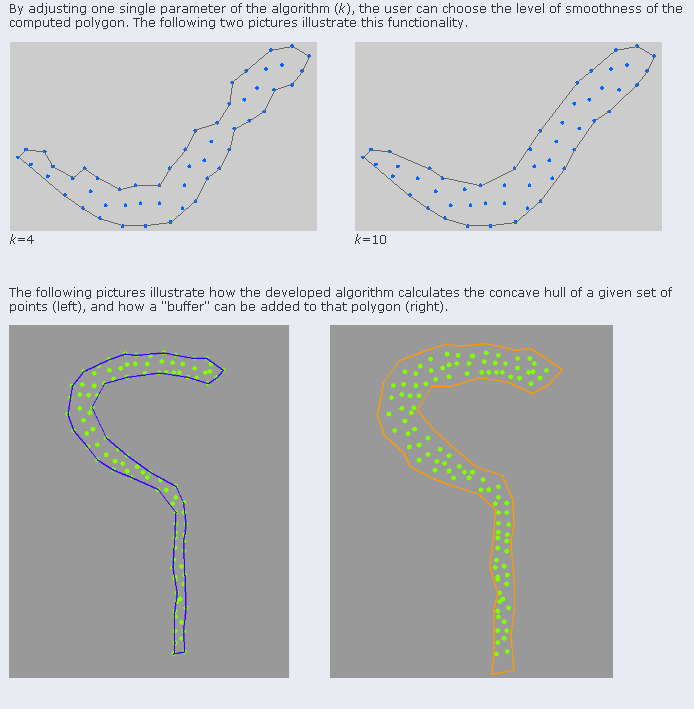
这里你可以要求一份论文的副本。

他们似乎是因为请求计算而计划提供在线服务，但我没有测试它，而且很可能它没有运行。

哈哈！

我认为维斯瓦林加算法可以适应这一目的-通过跳过删除三角形，以减少面积。

我有一个非常相似的问题:我需要一个膨胀的多边形简化。

我做了一个简单的算法，通过删除concav点(这将增加多边形大小)或删除凸边(两个凸点之间)和延长相邻边。在任何情况下，做这两种可能性中的一种将删除多边形上的一个点。

我选择移除导致最小面积变化的点或边缘。你可以重复这个过程，直到简化对你来说是可以的(例如，不超过200点)。

两个主要的困难是获得快速算法(避免计算顶点/边缘的变化两次并保持可能性排序)和避免在过程中插入自交点(不太容易做和解释可能，但计算复杂度有限)。

事实上，在仔细观察之后，这是一个类似的想法，维斯瓦林加与自适应的边缘去除。