具有符号输入的RecurrenceTable中的错误
我终于又在做我的n-point Pade code了,我遇到了一个以前没有发生过的错误。这件事的核心是围绕着这个代码:
zi = {0.1, 0.2, 0.3}
ai = {0.904837, 1.05171, -0.499584}
Quiet[ RecurrenceTable[ {A[0] == 0, A[1] == ai[[1]],
A[n+1]==A[n] + (z - zi[[n]]) ai[[n+1]] A[n-1]},
A, {n, Length@ai -1 } ],
{Part::pspec}]( Quiet的使用是必要的,因为Part抱怨zi[[n]]和ai[[n+1]],而n纯粹是象征性的。)代码本身是一个函数的一部分,我希望得到一个符号结果,因此z是一个Symbol。但是,当我运行上述代码时,会得到以下错误:
RecurrenceTable::nlnum1:
The function value {0.904837,0.904837+0. z} is not a list of numbers with
dimensions {2} when the arguments are {0,0.,0.904837}.注意术语{0.904837,0.904837+0. z},其中0. z未降为零。我需要做些什么来迫使它评估为零,因为它似乎是问题的根源?还有其他选择吗?
此外,对于经常出没在堆栈溢出中的Wolfram研究人员来说,作为对帮助系统的一般抱怨:在第7节中,RecurrenceTable::nlnum1是不可搜索的!同样,错误末尾的>>链接也不会带您到错误定义,而是带您到RecurrenceTable的定义,在那里常见的错误没有交叉引用。
编辑:在回顾了我的代码之后,我想出的解决方案是完全象征性地评估RecurrenceTable,包括初始条件。工作守则如下:
Clear[NPointPade, NPointPadeFcn]
NPointPade[pts : {{_, _} ..}] := NPointPade @@ Transpose[pts]
NPointPade[zi_List, fi_List] /; Length[zi] == Length[fi] :=
Module[{ap, fcn, rec},
ap = {fi[[1]]};
fcn = Module[{gp = #, zp, res},
zp = zi[[-Length@gp ;;]];
res = (gp[[1]] - #)/((#2 - zp[[1]]) #) &[Rest@gp, Rest@zp];
AppendTo[ap, res[[1]]];
res
] &;
NestWhile[fcn, fi, (Length[#] > 1 &)];
(*
The recurrence relation is used twice, with different initial conditions, so
pre-evaluate it to pass along to NPointPadeFcn
*)
rec[aif_, zif_, a_, b_][z_] :=
Evaluate[RecurrenceTable[
{A[n + 1] == A[n] + (z - zif[n])*aif[n + 1]*A[n - 1],
A[0] == a, A[1] == b},
A, {n, {Length@ap - 1}}][[1]]];
NPointPadeFcn[{zi, ap, rec }]
]
NPointPadeFcn[{zi_List, ai_List, rec_}][z_] /; Length[zi] == Length[ai] :=
Module[{aif, zif},
zif[n_Integer] /; 1 <= n <= Length[zi] := zi[[n]];
aif[n_Integer] /; 1 <= n <= Length[zi] := ai[[n]];
rec[aif, zif, 0, ai[[1]]][z]/rec[aif, zif, 1, 1][z]
]
Format[NPointPadeFcn[x_List]] := NPointPadeFcn[Shallow[x, 1]];和内置的插值函数一样,NPointPade做了一些预处理,并返回一个可以计算的函数,NPointPadeFcn。NPointPade所做的预处理除了预先评估递归关系外,还从zis和在这些点上的函数值生成ais的列表。当NPointPadeFcn被提供一个z值时,它通过向它提供适当的值来计算两个线性递归关系。
编辑:对于好奇的人来说,下面是运行中的NPointPade
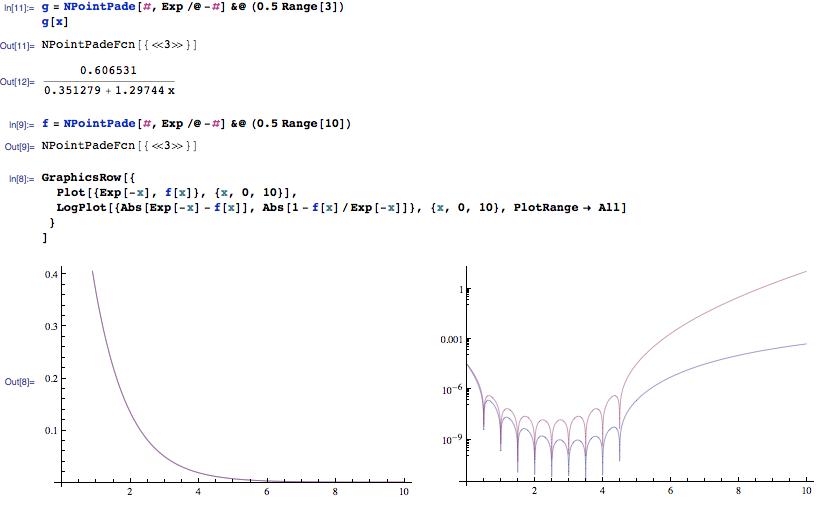
在第一个图中,很难区分这两个函数之间的区别,但是第二个图显示绝对(蓝色)和相对(红色)错误。正如所写的,创建一个20点的Pade需要很长的时间,所以我需要加快速度。但是,就目前而言,它起作用了。
回答 1
Stack Overflow用户
发布于 2011-04-26 16:36:43
您可以将部分提取隐藏在函数后面:
In[122]:= zi = {0.1, 0.2, 0.3};
ai = {0.904837, 1.05171, -0.499584};
In[124]:= zif[n_Integer] /; 1 <= n <= Length[zi] := zi[[n]]
aif[n_Integer] /; 1 <= n <= Length[ai] := ai[[n]]
In[127]:= RecurrenceTable[{A[0] == 0, A[1] == aif[1],
A[n + 1] ==
A[n] + (z - zif[n]) aif[n + 1] A[n - 1]}, A, {n, (Length@ai) - 1}]
Out[127]= {0.904837, 0.904837,
0.904837 - 0.271451 aif[4] + 0.904837 z aif[4]}
编辑
以下是解决这个问题的方法:
In[4]:= zi = {0.1, 0.2, 0.3};
ai = {0.904837, 1.05171, -0.499584};
In[6]:= zif[n_Integer] /; 1 <= n <= Length[zi] := zi[[n]]
aif[n_Integer] /; 1 <= n <= Length[ai] := ai[[n]]
In[8]:= Block[{aif, zif},
RecurrenceTable[{A[0] == 0, A[1] == aif[1],
A[n + 1] == A[n] + (z - zif[n]) aif[n + 1] A[n - 1]},
A, {n, 0, (Length@ai) - 1}]]
Out[8]= {0, 0.904837, 0.904837}Block用于在执行aif和zif时临时删除RecurrenceTable和zif的定义。然后,当Block退出时,恢复值,并计算RecurrenceTable的输出。
https://stackoverflow.com/questions/5793397
复制相似问题

