最大和最大团
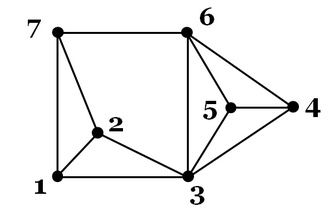
我正在做一个基于这个图像的练习。我发现最大的团大小是4,我对图论的概念有几个问题。
顾名思义,团是一个完整的子图,每个顶点都是连通的。这是否意味着,如果我计算三个集团,(3,4,5),(3,4,6),(3,5,6)和(4,5,6)将算作3-集团?或者我应该省略那些子图,因为它们是4团的一部分。
每个图都只有一个最大团吗?想象它在我的脑海中,我觉得这是可能有超过一个最大的集团。
本练习中的一个问题是,是否每个具有一个或多个节点的图必须至少有一个团。是有两个集团(只是一个边缘),还是每个集团应该形成一个封闭的形状?
我似乎不能画一个没有三个小集团的四小集团的例子,所以可以安全地假设每一个四小集团至少有一个三个小集团?我该如何在更大的范围内检查这样的事情呢?
回答 1
Stack Overflow用户
发布于 2011-10-07 06:27:02
首先,你提到的所有这三个集团实际上都是集团。
正如您所说,团是一个子图,其中所有节点都连接到所有其他节点。所以在你的例子中,(3,4,5)是一个集团,(3,4,5,6),以及(3)和(3,4) (这也回答了一些其他问题)。
关于最大的团,你当然可以有超过1,例如,如果你从你的图中取(3,4,5,6),把它复制到( 3',4',5',6'),把3和3‘连接起来,那么你的图中有2个4-团,但没有5-团。
另外,一个团的任何子图也是一个团,因为每个子图仍然满足所有节点连接到所有其他节点的要求。例如,在你的图中,(3,4,5,6)是一个4团.从那里取下任意3个节点,你就会得到一个3团.采取2,你就得到了一个2集团。事实上,不仅每一个4团都有至少1 3团,而且它有4 3团(也就是4C3)。
但是,请注意,有时候团被定义为有2个或更多(有时是3个或更多)节点,因为没有更好的词,任何较小的节点都是微不足道的。
https://stackoverflow.com/questions/7297374
复制相似问题

