如何用Mathematica 8找到加权二部图的最小边覆盖?
如何用Mathematica 8找到加权二部图的最小边覆盖?
提问于 2011-09-11 02:23:04
在图论中,我们使用匈牙利算法计算加权二部图的最小边覆盖(一组与每个顶点相关的边,即具有最小总权重的边)。
我发现在数学的新版本8中,有一个全新的图论函数包(从Graph[]开始)。但我没有找到任何功能来完成这项工作。我确实找到了一个名为FindEdgeCover[]的函数,它只能找到一个边缘覆盖,而不是最小的一个。
回答 1
Stack Overflow用户
发布于 2011-09-11 06:03:37
我做了一些实验,虽然没有文档化,但FindEdgeCover[]似乎做了您想做的事情。
例如,考虑:
h[list_] := CompleteGraph[4, EdgeWeight -> list]
FindEdgeCover[h@Range@6]
(*
-> {1->2,1->3,1->4}
*)但
FindEdgeCover[h@Reverse@Range@6]
(*
-> {1->2,3->4}
*)当然没有保证..。
编辑
这里有一些代码可以使用不同的加权邻接矩阵进行实验。
adj = {{\[Infinity], 1, 1, 1, 1}, {1, \[Infinity], 2, 2, 2},
{1, 2, \[Infinity], 2, 2}, {1, 2, 2, \[Infinity], 2},
{1, 2, 2, 2, \[Infinity]}}
g = WeightedAdjacencyGraph[adj];
g = WeightedAdjacencyGraph[adj, VertexShapeFunction -> "Name",
EdgeLabels ->
MapThread[
Rule, {EdgeList@g, AbsoluteOptions[g, EdgeWeight] /. {_ -> x_} -> x}],
GraphHighlight -> FindEdgeCover[g]]
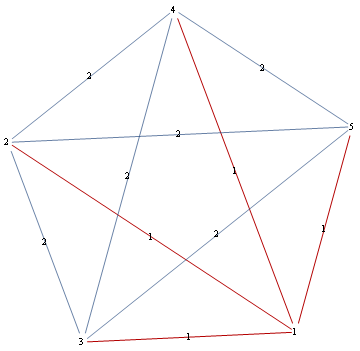
注意:代码一点也不好,但是我找不到使用EdgeLabels -> “EdgeWeight”的方法。我在this question上发了个帖子,想看看是否有人能做到。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/7375934
复制相关文章
相似问题

