什么是“让每个人都开心”的投票算法?
我正在寻找一种投票算法,它根据多数票和票数的组合来选出获胜者。
真实生活示例:
我们公司有一个麦片吧。我们有空间放三种不同的谷类。我们想让我们的员工投票决定他们想要哪种谷物。 我们不想严格地根据受欢迎程度来挑选前三名获奖者,因为可能有少数员工只能吃一种特定的麦片(不管是什么原因),我们想给他们尽可能的特别津贴。
根据下面的投票结果,这是我们希望算法给我们的结果。
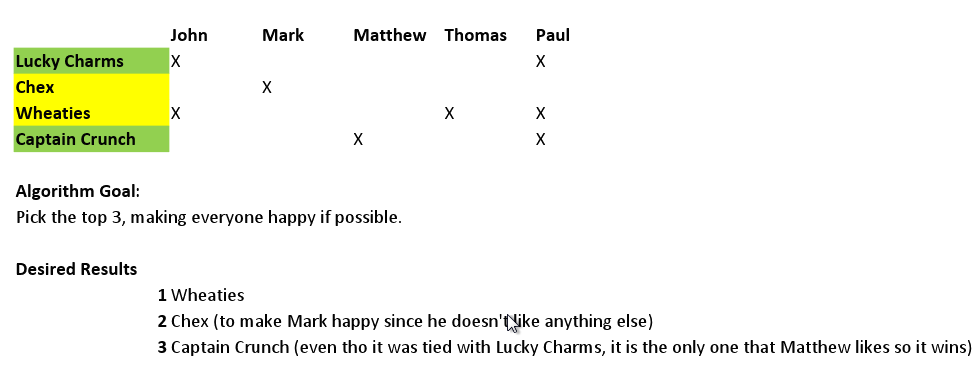
我在寻找一种算法来进行这种排序。如果你能至少提供我正在寻找的名字,那将是一个很大的帮助,因为我可以更好地寻找它。:)
谢谢!
回答 3
Stack Overflow用户
发布于 2011-12-14 23:12:16
您可能需要考虑霍尔婚姻定理和/或赋值问题的泛化。
这种模式的思想是创建一个二分图,其中节点是人和谷物,如果p投票给c,则在person p和谷物p之间有一个边缘。我们的目标是选择3种谷物,这样删除所有其他谷物所产生的图形是
- 连接(每个人将至少吃一种选定的谷物),以及
- 最大化每个人的最小/平均程度(最大限度/平均幸福)
相反,您可以把这看作是一个最大覆盖问题。在本例中,您有set C1,C2,...,Cm,其中Ci是一组喜欢谷物i的人。例如,以表格中列出的谷物和人员为例,您有
C1 = {1,5}
C2 = {2}
C3 = {1,4,5}
C4 = {3,5}让n是人数,这样Ci就是{1,2,...,n}的子集。目标是找到k集,使联合的基数最大化。如果存在多个解决方案,则选择一个将交叉口基数最小化的解决方案(最小化一个人主导的数量)或最大化重复最不频繁元素的次数(使最不快乐的人的幸福最大化)。
对于这个例子,覆盖所有元素的最小的k是k=3,它给出了唯一的解决方案C2,C3,C4。
不管你如何看待它,你都有一个NP问题,但是有一些已知的算法可以解决这些问题(查看维基百科的文章以获得参考)。
Stack Overflow用户
发布于 2011-12-14 20:39:45
没有一个完美的投票制度--见定理。有各种各样的尝试通过弯曲规则来克服这一点,包括投票。
接近范围投票的一个想法是给每个人12张选票,并允许他们按自己的意愿分配。看看你的例子,如果你假设有多种选择的人平均分配他们的12张选票-- 12x1,6x2,4x3或3x4 --那么我认为你得到了你想要的结果,幸运的钱尔斯得到了10张选票,其他的都得到了更多的选票。
Stack Overflow用户
发布于 2011-12-14 20:52:44
如果谷物的数量很小,你可以把你的问题看作是一个子集覆盖问题,用蛮力强迫你去找出什么样的配置才是最“幸福”的。
var max_happyness = -INF
for every subset {c1, c2, c3} of C:
max_hapyness = max(max_happyness, happyness(i1,i2,i3))然而,你仍然存在定义一个合适的幸福函数的问题。例如,你可以选择一个快乐函数,作为第一优先计算吃任何食物的人的数量。然后,作为第二优先事项,有多少人喜欢两种谷物,然后是那些喜欢三种谷物的人等等。
Pros: --如果您可以定义一个幸福度函数,这将给出保证的最佳结果。
Cons:,您必须能够定义一个幸福函数。
https://stackoverflow.com/questions/8511234
复制相似问题

