Mathematica [Sqrt[5+2 Sqrt[6]生成Sqrt[2]+Sqrt[3],但FullSimplify[-Sqrt[5+2 Sqrt[6]没有简化,为什么?
Mathematica [Sqrt[5+2 Sqrt[6]生成Sqrt[2]+Sqrt[3],但FullSimplify[-Sqrt[5+2 Sqrt[6]没有简化,为什么?
提问于 2011-12-19 21:10:14
我在玩(漂亮的)多项式x^4 - 10x^2 + 1。看看发生了什么:
In[46]:= f[x_] := x^4 - 10x^2 + 1
a = Sqrt[2];
b = Sqrt[3];
Simplify[f[ a + b]]
Simplify[f[ a - b]]
Simplify[f[-a + b]]
Simplify[f[-a - b]]
Out[49]= 0
Out[50]= 0
Out[51]= 0
Out[52]= 0
In[53]:= Solve[f[x] == 0, x]
Out[53]= {{x->-Sqrt[5-2 Sqrt[6]]},{x->Sqrt[5-2 Sqrt[6]]},{x->-Sqrt[5+2 Sqrt[6]]},{x->Sqrt[5+2 Sqrt[6]]}}
In[54]:= Simplify[Solve[f[x] == 0, x]]
Out[54]= {{x->-Sqrt[5-2 Sqrt[6]]},{x->Sqrt[5-2 Sqrt[6]]},{x->-Sqrt[5+2 Sqrt[6]]},{x->Sqrt[5+2 Sqrt[6]]}}
In[55]:= FullSimplify[Solve[f[x] == 0, x]]
Out[55]= {{x->Sqrt[2]-Sqrt[3]},{x->Sqrt[5-2 Sqrt[6]]},{x->-Sqrt[5+2 Sqrt[6]]},{x->Sqrt[2]+Sqrt[3]}}Sqrt[5-2 Sqrt[6]]等于Sqrt[3]-Sqrt[2]。
然而,Mathematica的FullSimplify并没有简化Sqrt[5-2 Sqrt[6]]。
问题:我是否应该使用其他更专门的函数来代数求解这个方程?如果是,哪一个?
回答 2
Stack Overflow用户
回答已采纳
发布于 2011-12-19 21:55:53
实际上,Solve并没有将所有根简化到最大值:
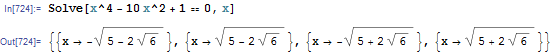
FullSimplify后处理步骤简化了两个根,并保留了另外两个根:
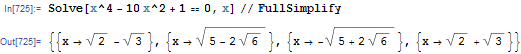
同样的情况最初发生在Roots上
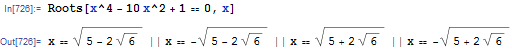
奇怪的是,现在FullSimplify简化了所有的根:
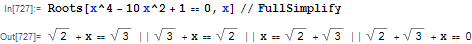
原因是,我假设,对于默认的ComplexityFunction,上面用嵌套根编写的一些解决方案在某种意义上比其他的更简单。
顺便说一句,FunctionExpand知道如何对付这些激进分子:
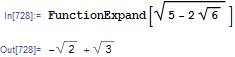
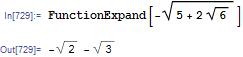
Stack Overflow用户
发布于 2011-12-19 21:51:51
FullSimplify[ Solve[x^4-10x^2+1==0,x]
,
ComplexityFunction ->
(StringLength[ToString[
InputForm[#1]]] & )]给出
{{x -> Sqrt[2] - Sqrt[3]}, {x -> -Sqrt[2] + Sqrt[3]}, {x -> -Sqrt[2] -
Sqrt[3]}, {x -> Sqrt[2] + Sqrt[3]}}页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/8567617
复制相关文章
相似问题

