数学中的Riffling卡
我的朋友向我提出了这个问题,我想在这里分享。
给出一副牌,我们把它分成两组,然后“交错”;让我们把这个操作称为‘分割-连接’。在产生的甲板上重复同样的操作。
例如,{ 1,2,3,4 }变为{ 1,2 } & { 3,4 } (split),我们得到{ 1,3,2,4 } (连接)
另外,如果我们有一个奇数的卡片,即{ 1,2,3 },我们可以像{ 1,2 } & { 3 } (大半第一)一样将它分开,从而导致{ 1,3,2 } (即n被拆分为Ceil[n/2] & n-Ceil[n/2])。
我朋友问我的问题是:
,需要多少这样的拆分连接才能收回原来的桥面?
这让我纳闷:
如果甲板上有n张卡片,那么在下列情况下所需的拆分连接数是多少:
- n是偶数?
- n是奇数?
- n是'2‘的幂?然后,我发现我们需要log (n) (基本2)号的split-joins...
- (Feel免费来探索不同的场景。)
是否有一个简单的模式/公式/概念,将n和所需的拆分连接数关联起来?
我相信,这是一个很好的东西,在数学探索,特别是,因为它提供了Riffle[]方法。
回答 4
Stack Overflow用户
发布于 2015-05-18 14:28:35
我知道的老问题,但奇怪的是,没有人提出一个实际的数学解决方案。
countrifflecards[deck_] := Module[{n = Length@deck, ct, rifdeck},
ct = 0;
rifdeck =
Riffle @@
Partition[ # , Ceiling[ n/2], Ceiling[ n/2], {1, 1}, {} ] &;
NestWhile[(++ct; rifdeck[#]) &, deck, #2 != deck &,2 ]; ct]这处理偶数和奇数案件:
countrifflecards[RandomSample[ Range[#], #]] & /@ Range[2, 52, 2]{1,2,4,3,6,10,12,4,8,18,6,11,20,18,28,5,10,12,36,12,20,14,12,23,21,8}
countrifflecards[RandomSample[ Range[#], #]] & /@ Range[3, 53, 2]{2,4,3,6,10,12,4,8,18,6,11,20,18,28,5,10,12,36,12,20,14,12,23,21,8,52}
您可以很容易地显示,如果您添加一张卡到奇数-大小写,额外的卡将停留在底部,不改变顺序,因此奇数的结果只是n+1偶数的结果。
ListPlot[{#, countrifflecards[RandomSample[ Range[#], #]]} & /@
Range[2, 1000]]
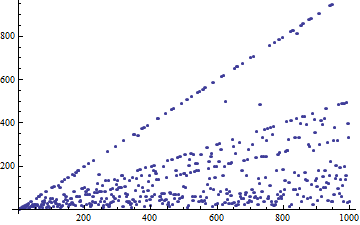
Stack Overflow用户
发布于 2012-01-09 12:36:45
引用MathWorld
.=.原顺序为1,2,4,3,6,10,12,4,8,18,6,11,.(Sloane's A002326),它只是2 (mod - n-1)的乘法阶.例如,从2**8=1 (mod 51) (Golomb 1961)开始,一个由52张牌组成的扑克牌在经过八次洗牌后返回到原来的状态。需要1,2,3,……的最少数目的卡2n。重新回到甲板的原始状态是1,2,4,3,16,5,64,9,37,6.(斯隆的A114894)
当n是奇数时,情况就没有得到解决。
请注意,这篇文章还包含了一个Mathematica notebook,其中包含了一些函数,可以用来探索“外乱”。
Stack Overflow用户
发布于 2012-01-09 14:16:57
如果我们有一个奇数的纸牌n==2m-1,并且如果在每次洗牌过程中,第一组包含m卡,第二组m-1卡,而这些组被加入,使得同一组中没有两张牌彼此相邻,那么所需的洗牌次数等于MultiplicativeOrder[2, n]。
为了说明这一点,我们注意到,在一次洗牌之后,处于位置的k已经转移到2k for 0<=k<m和2k-2m+1 for m<=k<2m-1,而k就是这样的0<=k<2m-1。编写模块n==2m-1 --这意味着新的职位是Mod[2k, n] for all 0<=k<n。因此,对于每一张卡片返回到它原来的位置,我们需要N洗牌,其中N是这样的,对于所有的0<=k<n,Mod[2^N k, n]==Mod[k, n]都是这样的,因此N是MultiplicativeOrder[2, n]的任何倍数。
请注意,由于对称性,如果我们以相反的方式分割甲板,结果将是完全相同的,也就是说,第一组总是包含m-1卡,第二组m卡。我不知道如果你交替的话会发生什么,例如,对于奇数洗牌,第一组包含m卡,对于偶数洗牌m-1卡。
https://stackoverflow.com/questions/8788446
复制相似问题

