问时间域上的零点感

EN

我有一个与Radon变换相关的任务，它包含一个子任务，它使用DFT重采样。

让我们考虑515像素长度的非周期性离散信号(图1)(例如，像素串)。在我的重采样实现中包含以下步骤：

1. 循环左移(图2)。
2. 向中心添加零点，以使信号长度变为2^n (在我们的例子中，1024-515 =我们必须加的509个零)(图3)。
3. 从这个信号中得到DFT (图4)。
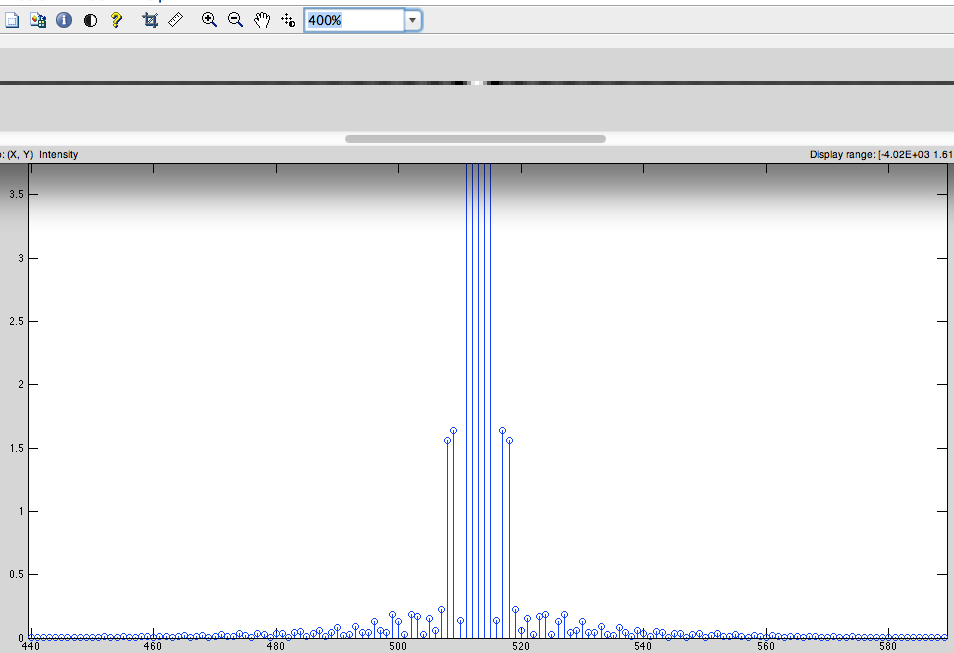
4. 循环右移。(用于将低频移至中心)(图5)

Fig.1

​

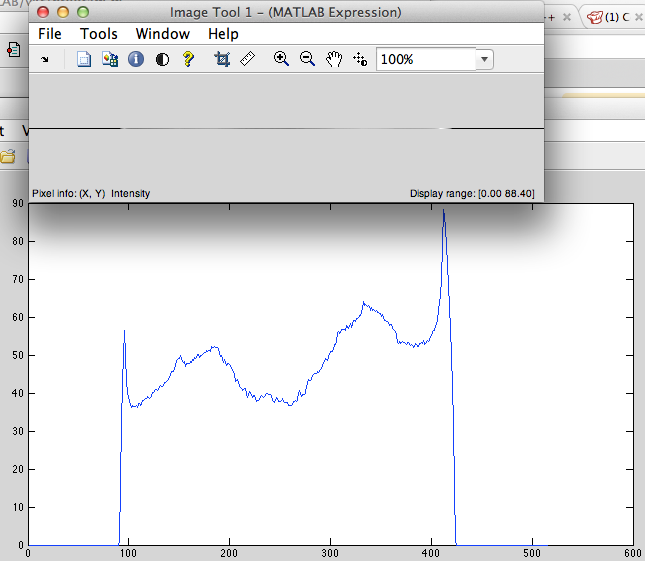
Fig.2

​

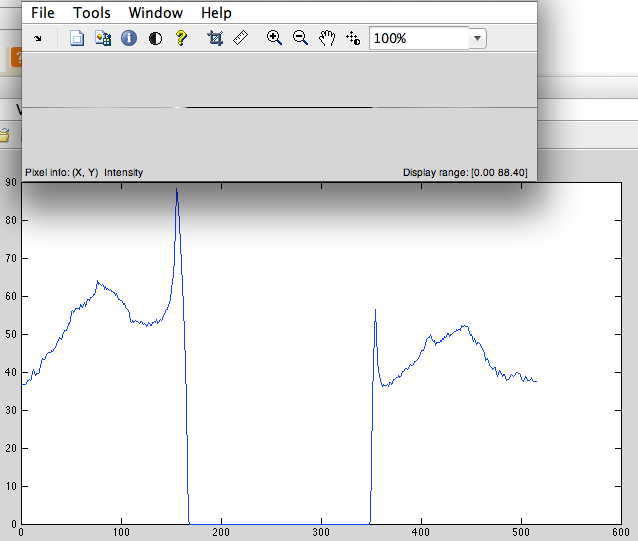
Fig.3

​

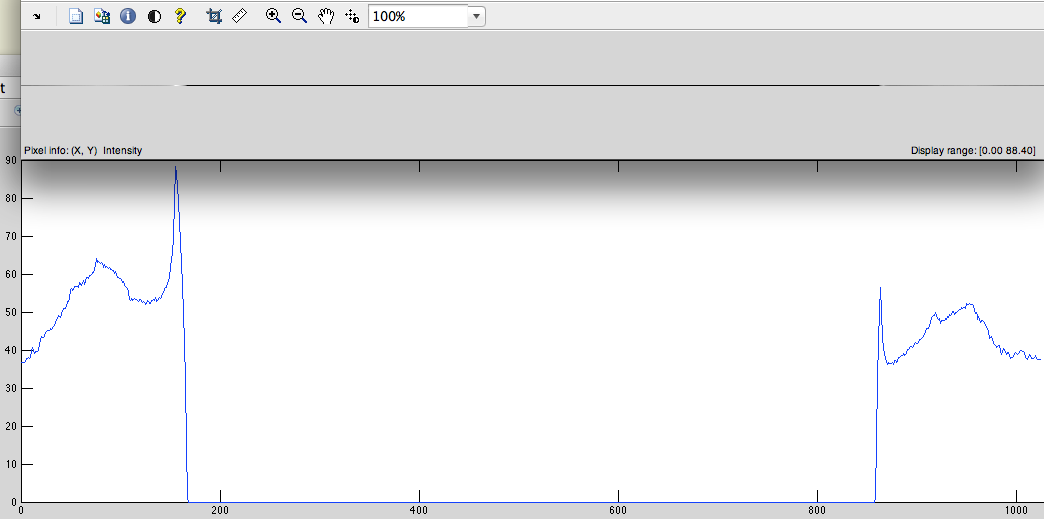
Fig.4

​

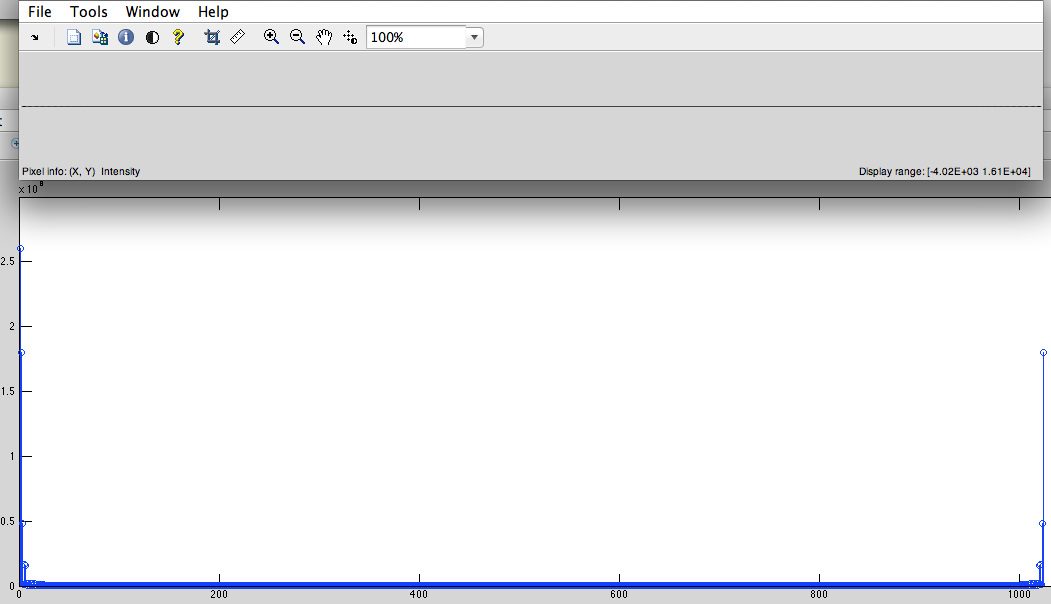
Fig.5

​

主要问题是：

为什么我们必须执行信号的循环移位，并在中心加零点？(我假设信号是周期性的)零加法使DFT谱内插，对吗？(我问，有人说不完全是这样)也许有人可以用简单的方式解释零加后的信号发生了什么。

我在Matlab中做了一些实验，发现任何其他的动作序列都不能给出所需的结果。

现在让我们考虑两种情况：

( a) (这个正确的变体)我们有非周期性离散信号(例如像素串)，它将被循环地移动到中心的左零和填充零点，然后得到DFT并将其移回。

​

( b)我们有一个非周期性离散信号(例如，像素的集合串)，它将从左到右填充零点，然后从这里得到DFT。

​

​

这些DFT光谱有什么不同？

我读过一些书，但没有找到零加法的答案。似乎只有自己的经验才能找到这一点。

书中的回答：

A. C. Kak和Malcolm Slaney，计算机断层成像原理，工业和应用数学学会，2001年，第25页