问轨迹插值与导数

EN

我正在分析二维平面中粒子的轨迹。这个轨迹通常由5到50个点(很少有更多)点(离散整数坐标)组成。我已经匹配我的数据集的点，以形成一个轨迹(因此，我有时间分辨率)。

我想对这个轨迹的曲率进行一些分析，不幸的是，我使用的分析框架不支持拟合轨道。据我所知，人们可以使用样条/贝塞尔曲线来完成这项工作，但我希望你的意见和/或建议，使用什么。

由于这只是我工作中的一个可选部分，我无法投入大量的时间来单独实现解决方案或理解复杂的框架。解决办法必须尽可能简单。

让我从一个可能的库中指定我需要的特性：

• 从不同的点创建轨迹
• 由于点是离散的，它应该插值它们的位置；只要轨迹和点之间的距离小于一个阈值，就不需要对所有点进行精确匹配。
• 对于任何给定的点，库都必须能够得到轨迹的导数。
• 如果库能够报告插值的质量级别(如chiSquare )，这将是有益的。

编辑：在阅读评论后，我想再添加一些：

轨迹与点完全匹配是不必要的。这些点是从像素矩阵的值中创建的，因此它们形成了一个离散的坐标矩阵，其空间分辨率受到每一给定距离像素数的限制。因此，点(放置在发射像素的中心)与粒子的实际轨迹不完全匹配。插值或拟合对我来说都很好，只要解能处理一个轨迹，这个轨迹很可能既不是双射的，也不是内射的。

因此，大多数传统的拟合方法(如多项式拟合或指数函数拟合)都不能满足我的准则。

此外，所有传统的拟合方法，我已经尝试了一个函数，它似乎很好地描述了轨道，但是当我们看到它们的一阶导数(或更高的分辨率)时，我们可以发现许多“微振荡”，这是(从我的解释中)将非直线函数拟合到(几乎)直线部分轨道的结果。

Edit2:在评论中有一些讨论，这些轨迹可能是什么样子。基本上，它可能有任何形状，长度和“卷曲”，虽然我试图排除轨道重叠或交叉在前面的步骤。下面我包含了两个例子；忽略有色框，它们只是原始像素矩阵值的表示。黑色圆点是我想要与轨迹匹配的点，因为你可以看到它们总是以像素为中心，因此可能只有离散(整数)值。

​

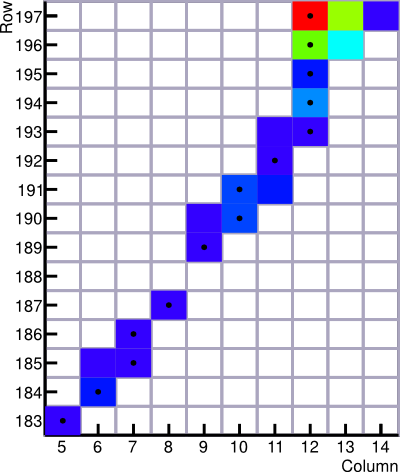
提前感谢您的帮助和贡献！