问对上界的更好猜测

EN

递归关系似乎产生了一个次指数和超线性计算时间，这意味着任何选择的基都将作为一个上界工作，给定一个足够大的n。

您选择的2^n是一个很好的答案，可能是他们在书中寻找的答案。这是一个简单的解决方案，即使对于非常小的n值也是有效的。(不过，我理解您为什么要问这个问题，因为即使对于中等大的T(n)，它的增长也比n快得多。)

给定T(1) = 1 (或其他常量)，递归方程给出n前几个值的运行时间如下。

T(1) = 1          n^1 = 2
T(2) = 4          n^2 = 4
T(3) = 11         n^3 = 8
T(4) = 19         n^4 = 16
T(5) = 35         n^5 = 32
T(6) = 52         n^6 = 64
T(7) = 78         n^7 = 128
T(8) = 105        n^8 = 256
T(9) = 149        n^9 = 512

我们可以看到，选择2^n作为上限对于所有值T(6)及以上都是有效的。

如果您想要一个比2^n更低的界限，您可以选择一个较低的基数(通过权衡，它只对较高数量的n有效)。但我必须补充一点，这基本上仍将是你已有的解决办法。

任何比一个大的基都可以，但是更具体一点，例如，我们可以看到递归方程T(n) = T(n-1) + T(n/2) + n被n>5的方程T(n) = T(n-1) + T(n-2)所限制。

这是与Fibonacci序列相同的递归关系，按照this问题答案中的步骤，它具有一个计算复杂度，将黄金比率(1+sqrt(5))/2 = 1,618与n的幂相匹配。

绘制我们可以看到的n的实际值，T(n)的值以((1+sqrt(5))/2)^n为界。从图中看，它似乎是值n=13及以上。

​

​

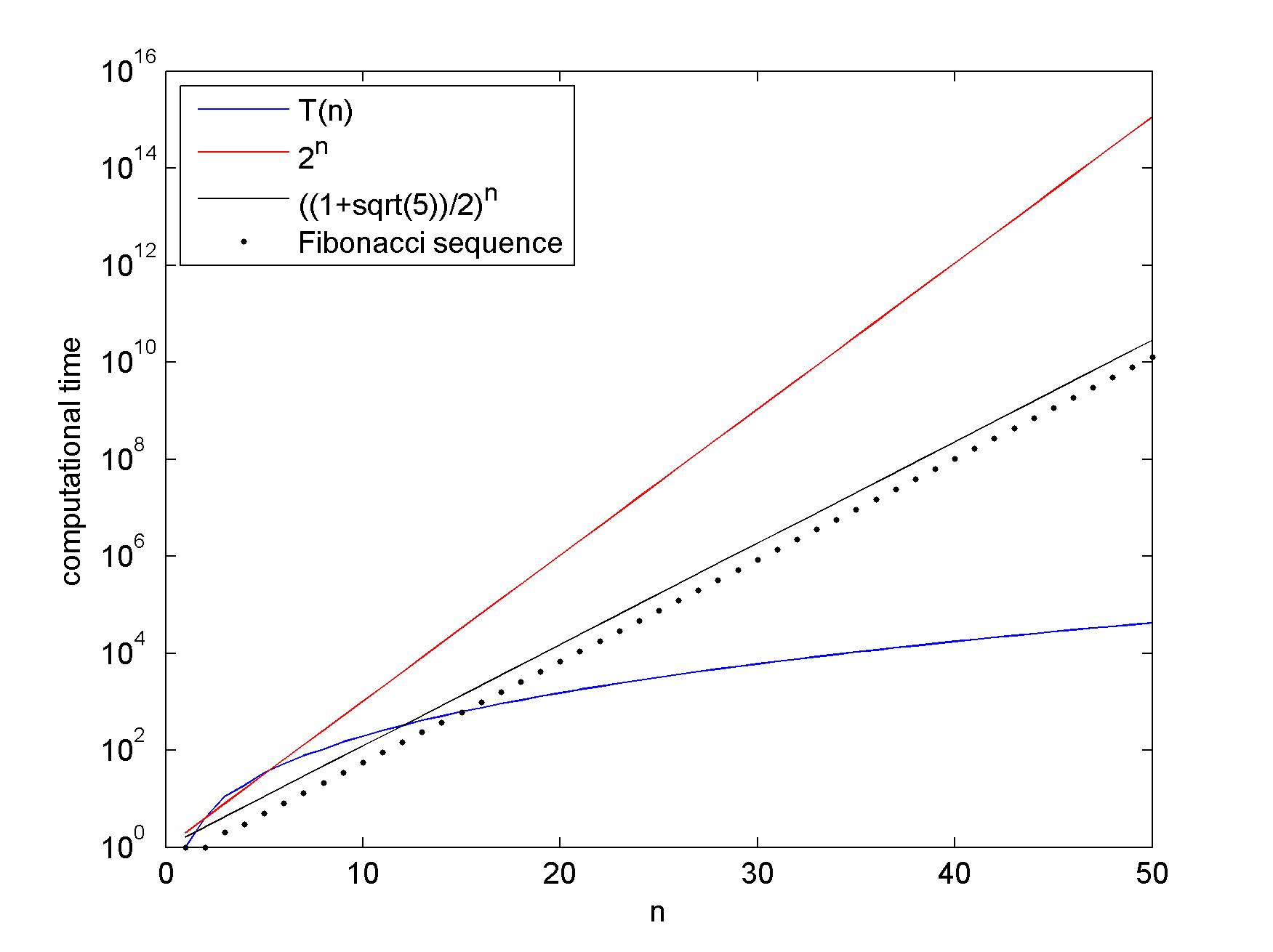
所有这一切，我已经考虑了一些关于用一些次指数函数来逼近运行时间。这似乎是不容易做到的，正如我说的，我相信你已经找到了预期的答案。