问分子动力学模拟:波动偶极子模型的实现

EN

我在对二氧化硅进行分子动力学模拟。一段时间前，我转向了波动的偶极子模型，经过了很大的努力，我仍然难以实现它。

简而言之，系统中的所有氧原子都是可极化的，它们的偶极矩取决于它们相对于系统中所有其它原子的位置。更特别的是，我使用TS势(http://digitallibrary.sissa.it/bitstream/handle/1963/2874/tangney.pdf?sequence=2)，其中偶极子在每一时间步骤都被迭代地发现。

这意味着，在计算作用在原子上的力时，我必须考虑到这个势能依赖于坐标。以前，我使用简单的成对势模型，所以我会设置程序，用通过微分势能表达式得到的解析公式来计算力。

现在我不知所措:如何实现这一新的潜力？在我发现的所有文章中，它们只给出了公式，但没有给出算法。在我看来，当我计算一个原子上的力时，我必须考虑这个原子的偶极子的变化，所有相邻原子的偶极子的变化，然后再考虑更多原子的偶极子的变化，等等，因为它们相互依赖。毕竟，正是由于这种相互依赖关系，偶极子才会在每一时间步骤中被迭代地发现。显然，我不能迭代计算每个原子的力，因为算法的计算复杂度太高了。我应该用一些简单的函数来解释偶极子的变化吗？这看起来也不是一个好主意，因为偶极子是迭代计算的，精度很高，然后，当它真正重要的地方(计算力)，我们会使用粗糙的函数？

那么我如何实现这个模型呢？另外，是否有可能像我以前那样解析地计算力，或者是否有必要使用导数的有限差分公式来计算它们？

我还没有在文献中找到我的问题的答案，但如果你知道一些文章，网站，或书籍，这些材料的突出显示，请指导我到那个来源。

谢谢您抽时间见我!

==================================================================================

更新：

谢谢你的回答。不幸的是，这不是我的问题。我没有问如何计算偶极子，而是如何计算力，因为这些偶极子随着运动而有很大的变化。

我试图以简单的方式计算力(没有考虑到偶极子之间的距离相互依赖，只需计算每个步骤上的偶极子，然后像那些偶极子是静态的那样计算这些力)，但是我得到的结果在物理上是不正确的。

为了分析这种情况，我建立了一个由两个原子组成的系统的模拟: Si和O，它们有相反的电荷，所以它们振荡。能量时间依赖图如下所示：

​

​

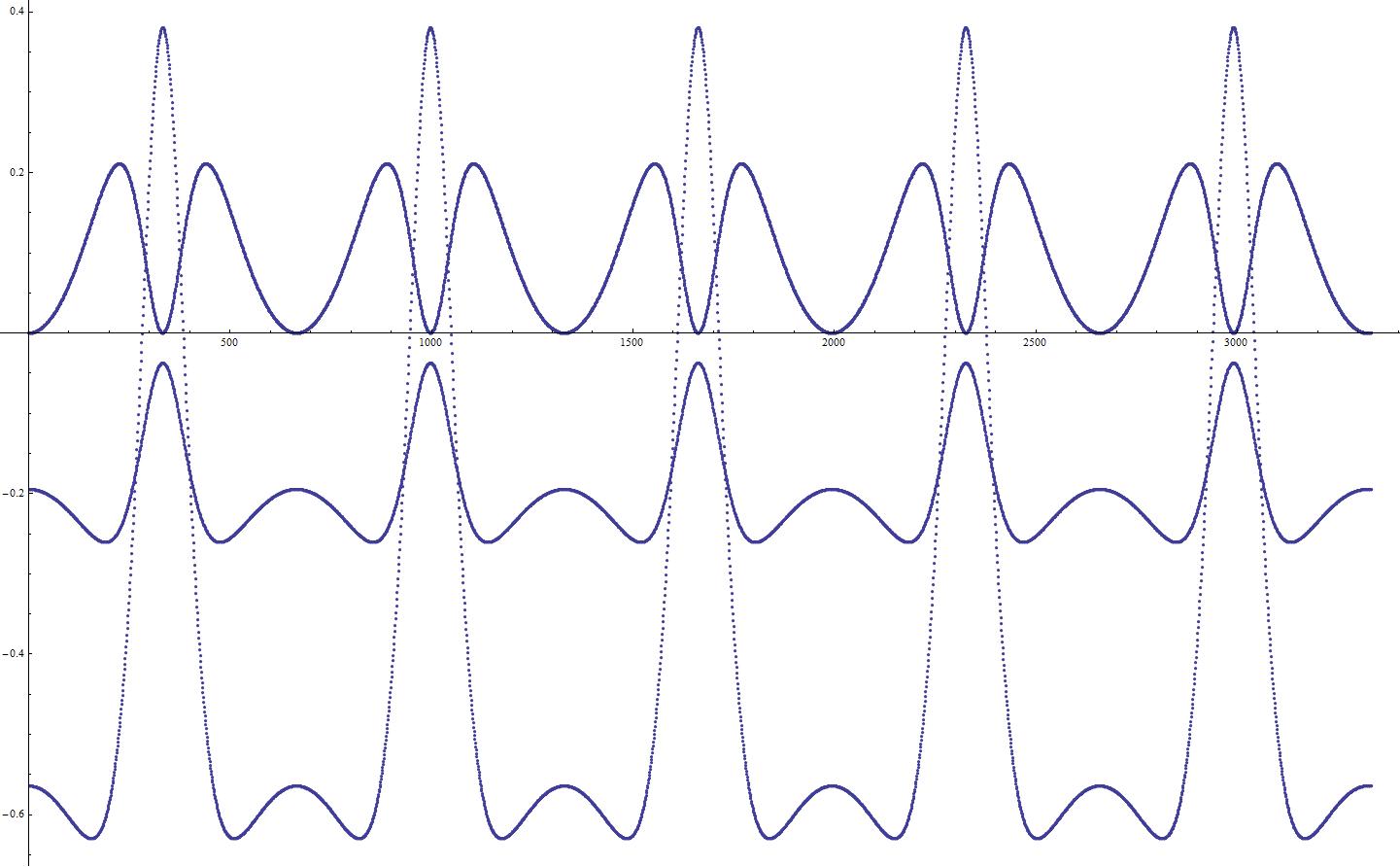
顶部的曲线代表动能，中间的曲线表示势能而不考虑偶极子相互作用，底部的曲线代表系统的势能，其中考虑了偶极子相互作用。

从这张图可以清楚地看到，系统正在做它不应该做的事情:爬上潜在的斜坡。所以我决定这是因为我没有考虑偶极矩，坐标依赖。例如，在给定的时间点，我们计算力，它们被定向，使两个原子相互移动。但是当我们把它们移向对方时，偶极矩就会发生变化，我们会发现我们最终得到的势能比以前更高了！在下一阶段，情况是一样的。

所以问题是，如何考虑这一影响，因为我所能想到的任何一种方法，要么计算过于激烈，要么过于粗糙。