问表示分类可信度

EN

你的自信是建立在旧的模型之上的。例如，如果您只是简单地应用一些基于角度(或边)数的规则，则有一些对象的多维表示：

feature 0, feature 1, ..., feature m

尼斯，统计方法

你可以根据你的经验结果来定义某种置信区间，例如。你可以将多维高斯分布与你对“矩形物体”的经验观测结果进行拟合，一旦你得到一个新的物体，你只需在高斯分布中检查这个值的概率，并且有你的信心(假设你的“观测”误差有正态分布，这是很有道理的)。

基于距离的简单方法

较少的统计方法是直接将模型的决策因子压缩到0,1中间值。例如，如果您只是在某个度量中度量从某个完美形状到新对象的距离(这会产生[0，inf))，那么您可以使用一些类似乙状结肠的函数来映射它。

conf( object, perfect_shape ) = 1 - tanh( distance( object, perfect_shape ) )

双曲切线将“压扁”到0,1间隔，唯一剩下的事情是选择一些缩放因子(因为它增长相当快)。

​

​

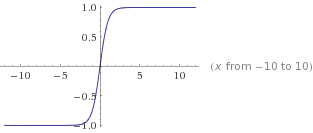
这种方法在数学上不那么有效，但与神经网络中的方法相似。

相对逼近

更多的概率方法也可以用你的距离度量来定义。如果你和你的每个“完美形状”都有距离，你可以计算出一个物体被归类为某类的概率，这种分类是随机的，可加工性与与完美形状的距离成反比。

dist(object, perfect_shape1) = d_1
dist(object, perfect_shape2) = d_2
dist(object, perfect_shape3) = d_3
...

                             inv( d_i )
conf(object, class_i) = -------------------
                          sum_j inv( d_j )

哪里

inv( d_i ) = max( d_j ) - d_i

结论

前两种思想也可以结合到第三种，利用所有类的知识。在您的特定示例中，第三种方法应该会对矩形和圆圈产生围绕0.5的信心，而在第一个示例中，它将更接近于0.01 (取决于您在“训练”集中会有多少个如此小的对象)，这表明了不同之处--前两种方法显示了您对分类为特定形状本身的信心，而第三种方法则显示出相对的自信(因此，当其他类的分类较高时，它可能会很低，而前两种方法则可以简单地回答“没有分类是自信的”)。

稍微建立在lejlot提出的基础上；我更喜欢使用Mahalanobis距离和一些压缩函数。Mahalanobis距离M(V, p)允许您测量分布V和点p之间的距离。

在您的例子中，我将使用每个类的“完美”示例来生成发行版V，而p是您想要信任的分类。然后，您可以使用以下内容作为您的信心区间。

1-tanh( M(V, p) )