python截面曲线拟合
python截面曲线拟合
提问于 2013-11-13 00:38:25
我有一组点描述一个简单的表面空腔/凸起的横截面。多项式逼近是足够的,但numpy.polyfit需要一定的程度。我想过几次不同程度的迭代,选择一个平均残差最小的迭代。是否有任何现有的功能,或更好的方法,以获得一个良好的曲线?计算时间非常重要:数据集很小(大约20分),但有数千个。
最初的任务是在一个非常离散的表面上找到这个空腔测地线--还有更简单的方法吗?
回答 1
Stack Overflow用户
回答已采纳
发布于 2013-11-13 02:01:09
除非我搞错了,否则你总能得到最小的,允许最大程度的残余物。如果允许优化器选择度d,那么它将选择无限大的d,尽管在实际中,当d = dof ( dof )是适合的自由度数(基本上是数据点的数目)时,它将停止,此时将有零的残差。
如果您对fit的真正函数形式并不感兴趣,只想要曲线,您可以使用 module进行插值,这对于您可能正在做的事情的类型来说更加灵活。
如果速度很重要,格式也没那么重要,那就试试np.polynomial.polynomial.polyfit和scipy.interpolate.UnivariateSpline,看看哪个更快。
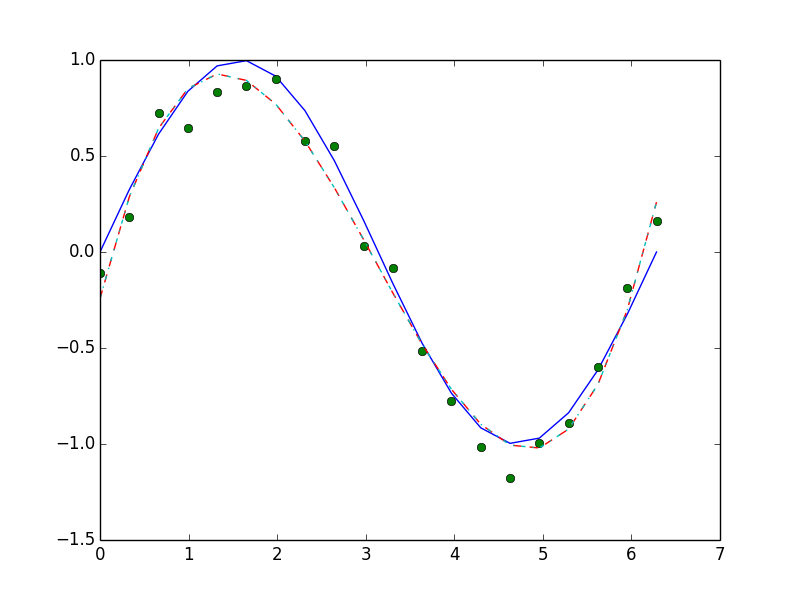
在我看来,样条的速度要快得多,就我的例子而言,它们给出了同样的结果(记住,样条基本上只是多项式串在一起的)。
import numpy as np
from numpy.polynomial import polynomial as poly
from scipy import interpolate as interp
import matplotlib.pyplot as plt
n = 20
x = np.linspace(0, 2*np.pi, n)
a = np.sin(x) + np.random.uniform(-.2, .2, n)
s = interp.UnivariateSpline(x, a)
p = poly.polyfit(x, a, 3)
p = poly.Polynomial(p)
plt.figure()
plt.plot(x, np.sin(x), '-', x, a, 'o', x, s(x), '--', x, p(x), '.-')
In [32]: timeit s = interp.UnivariateSpline(x, a)
10000 loops, best of 3: 22.1 µs per loop
In [33]: timeit p = poly.Polynomial(poly.polyfit(x, a, 3))
1000 loops, best of 3: 392 µs per loop
In [34]: timeit p = poly.polyfit(x, a, 3)
1000 loops, best of 3: 311 µs per loop包括评价:
In [35]: timeit interp.UnivariateSpline(x, a)(x)
10000 loops, best of 3: 44.9 µs per loop
In [37]: timeit poly.Polynomial(poly.polyfit(x, a, 3))(x)
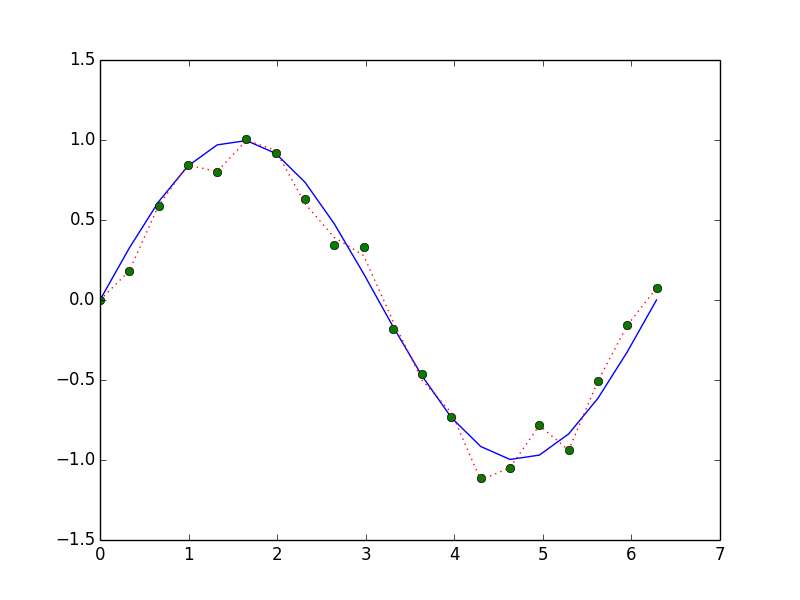
1000 loops, best of 3: 470 µs per loop为了好玩,为了说明过拟合的概念,这是一个带有d >= dof的多项式。
p = poly.Polynomial(poly.polyfit(x, a, x.size-1))
plot(x, np.sin(x), '-', x, a, 'o', x, p(x), ':')
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/19942995
复制相关文章
相似问题

