从R中未知密度的分位数生成随机样本
从R中未知密度的分位数生成随机样本
提问于 2013-12-11 00:44:04
如何从未知密度f(x)的分位数中生成随机样本数据,用于R中0和4之间的0和4?
f = function(x) ((x-1)^2) * exp(-(x^3/3-2*x^2/2+x))回答 3
Stack Overflow用户
回答已采纳
发布于 2013-12-11 02:33:41
如果我正确理解你(??)你想要生成随机样本,它的密度函数是由f(x)给出的。一种方法是从均匀分布U[0,1]生成一个随机样本,然后将这个样本转换成密度。这是使用f的逆of来完成的,这是以前描述过的一种方法,here。
所以,让
f(x) = your density function,
F(x) = cdf of f(x), and
F.inv(y) = inverse cdf of f(x).在R代码中:
f <- function(x) {((x-1)^2) * exp(-(x^3/3-2*x^2/2+x))}
F <- function(x) {integrate(f,0,x)$value}
F <- Vectorize(F)
F.inv <- function(y){uniroot(function(x){F(x)-y},interval=c(0,10))$root}
F.inv <- Vectorize(F.inv)
x <- seq(0,5,length.out=1000)
y <- seq(0,1,length.out=1000)
par(mfrow=c(1,3))
plot(x,f(x),type="l",main="f(x)")
plot(x,F(x),type="l",main="CDF of f(x)")
plot(y,F.inv(y),type="l",main="Inverse CDF of f(x)")
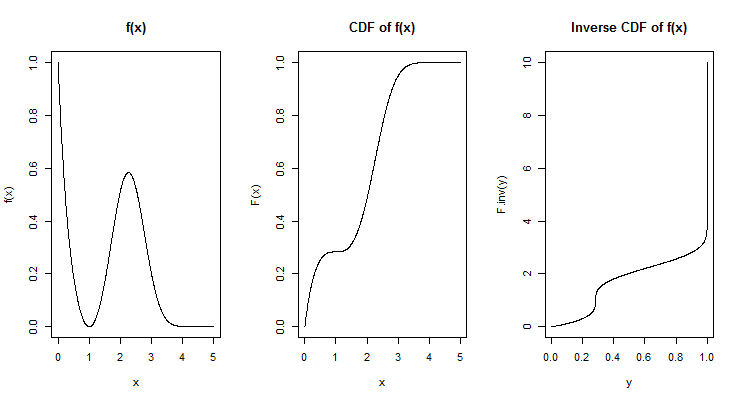
在上面的代码中,由于f(x)只在[0,Inf]上定义,所以我们将F(x)计算为从0到x的f(x)积分,然后在F-y上使用uniroot(...)函数进行反演。需要使用Vectorize(...),因为与几乎所有的R函数不同,integrate(...)和uniroot(...)不对向量进行操作。您应该查找这些函数上的帮助文件以获得更多信息。
现在,我们只生成一个从X中提取的随机样本U[0,1],并使用Z = F.inv(X)进行转换。
X <- runif(1000,0,1) # random sample from U[0,1]
Z <- F.inv(X)最后,我们证明了Z确实是以f(x)的形式分发的。
par(mfrow=c(1,2))
plot(x,f(x),type="l",main="Density function")
hist(Z, breaks=20, xlim=c(0,5))
Stack Overflow用户
发布于 2013-12-11 03:12:34
拒绝抽样是非常容易的:
drawF <- function(n) {
f <- function(x) ((x-1)^2) * exp(-(x^3/3-2*x^2/2+x))
x <- runif(n, 0 ,4)
z <- runif(n)
subset(x, z < f(x)) # Rejection
}不是最有效率的,但它能完成任务。
Stack Overflow用户
发布于 2013-12-11 12:32:17
使用sample。从您现有的函数f中生成概率向量,并进行适当的规范化。从“帮助”页面:
sample(x, size, replace = FALSE, prob = NULL)
Arguments
x Either a vector of one or more elements from which to choose, or a positive integer. See ‘Details.’
n a positive number, the number of items to choose from. See ‘Details.’
size a non-negative integer giving the number of items to choose.
replace Should sampling be with replacement?
prob A vector of probability weights for obtaining the elements of the vector being sampled.页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/20508400
复制相关文章
相似问题

