Minimax算法解释
我正在查看Minimax算法的伪代码:
Function Minimax-Decision(state) returns an action
;inputs: state (current game state)
;'E' means element of, 'a' is the action
return a E Actions(state) maximizing Min-Value(Result(a, state))
Function Max-Value(state) returns a utility value
if Terminal-Test(state) then return Utility(state)
v <-- -infinity
for a, s in Successors(state) do v <-- Max(v, Min-Value(s))
return v
Function Min-Value(state) returns a utility value
if Terminal-Test(state) then return Utility(state)
v <-- infinity
for a, s in Successors(state) do v <-- Min(v, Max-Values(s))
return v我想我知道Minimax算法是如何工作的。从实用程序分数开始,从自下而上开始填写“分数”值。在Max的节点中,最大的是它的子节点,Min的节点是最小的。Max预测,Min将总是尝试将Max置于下一回合可能出现的最糟糕的位置,并且利用这一知识,Max试图使最佳移动成为可能。
所以:用最高命令,从上面,从上面
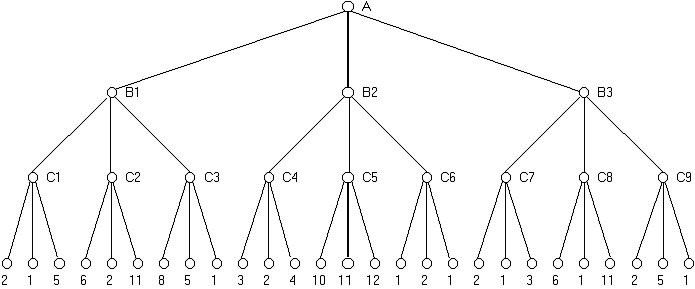
( 1)马克斯想为自己做最好的选择(最大的效用),所以C1=5,C2=11,C3=8等等
2) Max预测,Min会把Max放在最坏的位置(将Max限制在最小的效用),所以B1=5,B2=2,B3=3
( 3) Max想要做最好的动作,所以A=B1=5
有什么让我困惑的伪码是双重递归,以及v的目的,谁能为我打破这个吗?
谢谢大家的阅读!
回答 1
Stack Overflow用户
发布于 2014-02-03 05:56:47
我认为,您可以通过归纳的非正式证据来理解这段代码,它适用于深度为d的树。
对于深度1,您只有一个节点,Min值和最大值都返回该节点的实用程序。
对于深度d>1,首先考虑最小值.V以无穷大开始,因此在第一次调用Min(v,Max-Value(s))时,v被设置为由Max计算的子节点的实用程序,因为这是Max在Min之后的回合,我们知道通过归纳,它是正确的,因为它的深度为d-1。(此调用相当于赋值,因为v <=无穷大),以后在这个例程中对Min(v,Max-Value)的调用最终会计算节点传入的所有子节点的最大值的最小值。因此,Min-Value最终计算出传入节点的所有子节点的最小实用程序,即当Min移动时,该节点的值到Min。
最大值的参数和最小值的参数是一样的,所以归纳法告诉你,对于任意深度的树,最小值和最大值都返回给你传递给它们的节点的值,当是Max或Min的时候,移动和做出与该节点相关的选择。
您还可以通过归纳显示此代码所做的工作与您所描述的相同。
因此出现了双递归,因为它允许Max和Min在从树叶上走到树上时交替转弯,v是临时的,用来计算出树的所有子节点的最小值或最大值。
https://stackoverflow.com/questions/21519112
复制相似问题

