问OpenCV中的转换概念

EN

( 1)这不是关于OpenCV的问题，而是关于数学的问题。将仿射变换应用于(x，y)点意味着：

x_new = a*x + b*y + c;
y_new = d*x + e*y + f;

因此仿射变换有6个自由度: a，b，c，d，e，f，它们存储在2x3矩阵中: a，b，c在第一行，d，e，f在第二行。通过矩阵和向量的乘积，你可以将变换应用到一个点上。

(x，y)的透视变换是：

z = g*x + h*y + 1;
x_new = (a*x + b*y + c)/z;
y_new = (d*x + e*y + f)/z;

正如你所看到的，它有8个自由度，存储在3x3矩阵中。第三行是g，h，1。

有关此表示为何如此方便的更多信息，请参见齐次坐标。

2)仿射变换也称为“弱透视”变换:如果你从不同的角度看某一场景，但场景的大小相对于与摄像机的距离相对较小(即平行线或多或少保持平行)，那么你可以使用仿射变换。否则，透视转换将是必需的。

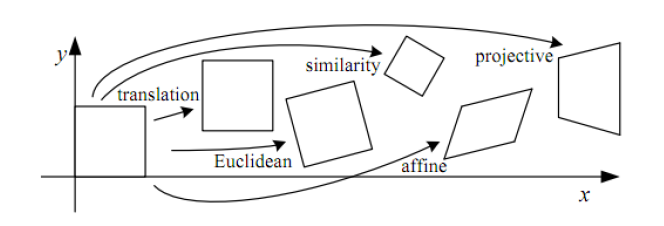
最好考虑一个空洞化的变换家族，这样你才能真正记住什么是什么。让我们从最简单的到复杂的: 1. 欧几里得-这是平面上的刚性旋转加上平移。基本上，你能做的就是把一张纸放在桌子上。2. 相似性--可以旋转、平移和缩放的更一般的变换(因此是非刚性的)；3. 仿射--增加另一个操作--剪切--它将从一个矩形生成一个平行四边形。这种纯粹发生在正投影或物体从远距离观察时(相对于它们的大小)；平行线仍然保留。4. 单形或透视变换--最一般的变换，它将使矩形(即两边不同的剪切量)形成梯形。这种情况发生在从近距离投影平面物体时。还记得火车是如何在无穷远处汇合的吗？因此，名称透视图。这也意味着，与其他转换不同的是，我们必须在某个时候应用一个除法。这就是第三行从齐次坐标转换为笛卡尔坐标时所做的事情，我们除以最后第三行的值。

这种变换是唯一不能用线性代数进行最优计算且需要非线性优化的变换。在摄像机投影中，有三种情况发生: 1.平面与图像之间；2.相机旋转但不平移时，任意图像之间；3.变焦过程中。换句话说，每当一个平面摄像机传感器穿过相同的光路，你就会有一个同调。

​