求直线上点的坐标
求直线上点的坐标
提问于 2014-03-05 06:24:16
这应该是件容易的事。我试图找出直线上一个点的坐标。我正在MATLAB中实现。我知道,端点的坐标和距离点的距离。
我使用以下公式计算坐标(请注意,我不能使用中点公式,因为距离可能会变化)。
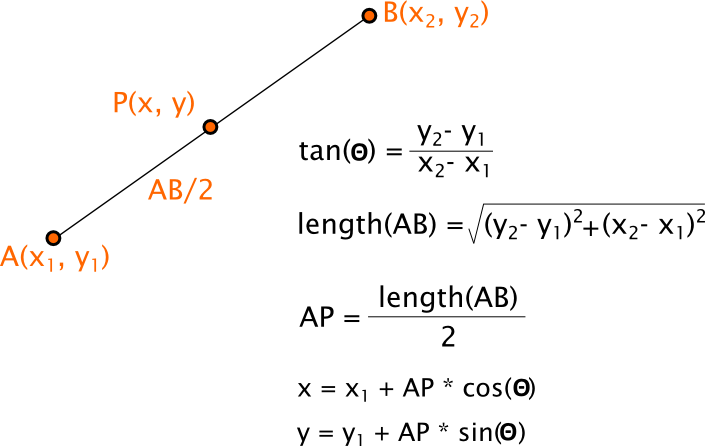
当斜率为负值时,我得到了错误的结果。你能否建议,使用这个公式需要考虑的条件是什么?我也不知道其他的公式。
回答 3
Stack Overflow用户
回答已采纳
发布于 2014-03-05 07:13:15
您的解决方案没有什么问题,但是当您使用arctangent来计算角度θ时,您需要考虑象限的模糊性。
在大多数编程语言中,有一个很好的解决方案:atan2。因此:
%// Your points (fill in any values)
A = [-10 0];
B = [-1 -1];
%// Use atan2!
th = atan2( B(2)-A(2) , B(1)-A(1) );
%// Distance from A to the point of interest
AP = sqrt( (B(2)-A(2))^2 + (B(1)-A(1))^2 ) / 2;
%// The point of interest
C = [
A(1) + AP*cos( th )
A(2) + AP*sin( th )];
%// Verify correctness with plots
figure(1), clf, hold on
line([A(1); B(1)], [A(2); B(2)])
plot(...
A(1), A(2), 'r.',...
B(1), B(2), 'b.',...
C(1), C(2), 'k.', 'markersize', 20)通常,无论何时何地需要使用arctangent,请使用atan2而不是atan。普通的atan只适用于您不知道部门y/x的各个组件的情况。
请注意,您的解决方案不能扩展到3D,而其他人提出的向量解决方案则是。所以总的来说,我建议你们开始研究向量。它不仅在许多情况下简单得多,而且更多用途。
Stack Overflow用户
发布于 2014-03-05 06:38:29
对于这么简单的任务来说,这个解决方案太复杂了。使用直接矢量计算:
function P = point_on_line(A, B, AP)
D = B - A;
P = A + D / norm(D) * AP;
end像这样打电话:
P = point_on_line([x1 y1], [x2 y2], len);
x = P(1);
y = P(2);问你是否需要任何澄清。
Stack Overflow用户
发布于 2014-03-05 06:38:21
这是解决方案的错误方法,因为解决方案并不是唯一的。在你的直线上有两个点,距离A点有相同的距离:一个向左,另一个向右。
解决这个问题的方法是无限的,我更喜欢向量表示法。
矢量ab是一个2x1 matlab矩阵:
ab = B-A abN是归一化向量
abN = ab/norm(ab) 从A到abN方向的距离d(在您的例子中是AP)是:
A + abN*d希望能帮上忙。
奥哈德
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/22190193
复制相关文章
相似问题

