使用带有逻辑条件的循环生成带有python的字符串,对联接函数替代产生问题吗?
使用带有逻辑条件的循环生成带有python的字符串,对联接函数替代产生问题吗?
提问于 2014-03-11 01:55:23
我编写了一个函数来生成拉格朗日插值表达式。
所以我得到了:
def polinomioLagrange(Xs, Ys, t):
for k in range(len(Xs)):
if k >0:
expresion = expresion + '+' + str(Ys[k]) + '*'
elif k==0:
expresion = expresion + str(Ys[k]) + '*'
expresion = expresion + '('
for i in range(len(Xs)):
if k==i:
continue
expresion = expresion + '(' + '3' + '-' + str(Xs[i]) + ')'
if k != len(Xs)-1 and i!= len(Xs)-1:
expresion=expresion+'*'
expresion = expresion + '/'
for i in range(len(Xs)):
if k==i:
continue
expresion = expresion + '(' + str(Xs[k]) + '-' + str(Xs[i]) + ')'
if i != len(Xs)-1 and k != len(Xs)-1:
expresion=expresion+'*'
print expresion我正在调用它,例如:polinomioLagrange([0,1,2,4],[7,0,-1,63],3)和我得到的输出类似于:
7*((3-1)*(3-2)*(3-4)/(0-1)*(0-2)*(0-4))+0*((3-0)*(3-2)*(3-4)/(1-0)*(1-2)*(1-4))+-1*((3-0)*(3-1)*(3-4)/(2-0)*(2-1)*(2-4))+63*((3-0)(3-1)(3-2)/(4-0)(4-1)(4-2))可以看出,在最后一学期没有星号:
63*((3-0)(3-1)(3-2)/(4-0)(4-1)(4-2))那是因为
if k != len(Xs)-1 and i!= len(Xs)-1:
expresion=expresion+'*'但是我真的玩过索引,结果并不完全是我想要的:
7*((3-1)*(3-2)*(3-4)/(0-1)*(0-2)*(0-4))+0*((3-0)*(3-2)*(3-4)/(1-0)*(1-2)*(1-4))+-1*((3-0)*(3-1)*(3-4)/(2-0)*(2-1)*(2-4))+63*((3-0)*(3-1)*(3-2)/(4-0)*(4-1)*(4-2))什么样的逻辑条件可以完成这项工作,更重要的是,使用更复杂的python函数(如join )来完成它,最简单的方法是什么?
我得到的最接近,循环和变化的逻辑条件是:
if i != len(Xs)-1:
expresion=expresion+'*'得到:
7*((3-1)*(3-2)*(3-4)/(0-1)*(0-2)*(0-4))+0*((3-0)*(3-2)*(3-4)/(1-0)*(1-2)*(1-4))+-1*((3-0)*(3-1)*(3-4)/(2-0)*(2-1)*(2-4))+63*((3-0)*(3-1)*(3-2)*/(4-0)*(4-1)*(4-2)*)几乎修正了,但...)*/(...和...4-2)*)除外
为了记录在案,这就是我要编码的内容:
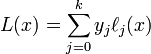
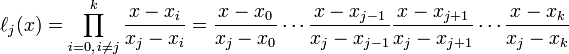
回答 1
Stack Overflow用户
回答已采纳
发布于 2014-03-11 02:49:34
我觉得你让事情变得比需要的困难多了。与其构建字符串,不如简单地构建符号表达式。我们可以直接实现l和L:
from sympy import Symbol, prod
def lag_l(xx, j):
x = Symbol("x")
parts = ((x - x_i) / (xx[j] - x_i) for i, x_i in enumerate(xx) if i != j)
return prod(parts)
def lag_L(xx, yy):
return sum(y*lag_l(xx, j) for j, y in enumerate(yy))
def lag_fn(xx, yy, x):
return lag_L(xx, yy).subs({'x': x})在此之后,我们可以得到基本函数:
>>> lag_l([1,2,3], 0)
(-x + 2)*(-x/2 + 3/2)
>>> lag_l([1,2,3], 1)
(-x + 3)*(x - 1)
>>> lag_l([1,2,3], 2)
(x/2 - 1/2)*(x - 2)全内插多项式:
>>> lag_L([1,2,3],[1,4,9])
(-x + 2)*(-x/2 + 3/2) + 4*(-x + 3)*(x - 1) + 9*(x/2 - 1/2)*(x - 2)我们可以调用这个函数(这里包装为lag_fn):
>>> lag_fn([1,2,3],[1,4,9], 3)
9。。当然,插值多项式可以简化很多:
>>> from sympy import simplify
>>> simplify(lag_L([1,2,3],[1,4,9]))
x**2页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/22314956
复制相关文章
相似问题

